更多有关于 “ 区块链 ” 的文章,请点击这里。
精英在做啤酒,平民在吹泡沫,骗子在割韭菜。
Bitcoin: A Peer-to-Peer Electronic Cash System
Satoshi Nakamoto
satoshin@gmx.com
www.bitcoin.org
Abstract. A purely peer-to-peer version of electronic cash would allow online payments to be sent directly from one party to another without going through a financial institution. Digital signatures provide part of the solution, but the main benefits are lost if a trusted third party is still required to prevent double-spending. We propose a solution to the double-spending problem using a peer-to-peer network. The network timestamps transactions by hashing them into an ongoing chain of hash-based proof-of-work, forming a record that cannot be changed without redoing the proof-of-work. The longest chain not only serves as proof of the sequence of events witnessed, but proof that it came from the largest pool of CPU power. As long as a majority of CPU power is controlled by nodes that are not cooperating to attack the network, they’ll generate the longest chain and outpace attackers. The network itself requires minimal structure. Messages are broadcast on a best effort basis, and nodes can leave and rejoin the network at will, accepting the longest proof-of-work chain as proof of what happened while they were gone.
比特币白皮书:一种点对点的电子现金系统
中本聪
satoshin@gmx.com
www.bitcoin.org
摘要:一个完全通过点对点技术实现的电子现金,它使得在线支付能够直接由一方发起并支付给另外一方,中间不需要通过任何的金融机构。虽然数字签名( Digital signatures )部分解决了这个问题,但是如果仍然需要第三方的支持才能防止双重支付( double-spending )的话,那么这种系统也就失去了存在的价值。我们( we )在此提出一种解决方案,使用点对点网络来解决双重支付的问题。该网络通过散列运算( hashing )对全部交易加上时间戳( timestamps ),并将这些交易合并进一个不断延伸的基于散列运算的工作量证明( proof-of-work )的链条作为交易记录,除非重新完成全部的工作量证明,否则形成的交易记录将不可更改。最长的链条不仅将作为被观察到的事件序列( sequence )的证明,而且被看做是来自 CPU 计算能力最大的集合( pool )。只要大多数的 CPU 计算能力都没有打算合作起来对全网进行攻击,那么诚实(或可信)的节点将会生成最长的、超过攻击者的链条。这个系统本身需要的基础设施非常少。信息尽最大努力在全网传播即可,节点( nodes )可以随时离开和重新加入网络,并将最长的工作量证明链条作为在该节点离线期间发生的交易的证明。
注解:
1 、Bitcoin / bitcoin :
比特币,一种点对点的电子现金系统。在标题中,比特币是一个系统,比特币不应该是一个币吗?这里就涉及到英文的首字母大小写的不同意思了。
- Bitcoin :一种点对点的电子现金系统,指的是比特币的网络系统,货币支付系统( electronic cash system )。
- bitcoin :是比特币网络系统中的记账单位,即我们在交易所中买卖的比特币( electronic cash )。
2 、digital signatures / double-spending / Hash / proof-of-work / timestamp :
digital signatures :数字签名。上一句还在讲点对点现金,怎么下一句就跳到了数字签名了?在本文 “ 交易 ” 这一章就有这么一句话:
We define an electronic coin as a chain of digital signatures.
中本聪将电子货币定义为一连串的数字签名,也就是说数字签名在这里就是指代电子现金。如需了解 “ 数字签名 ” 的更多内容,请点击这里。
double-spending :双重支付、双花。在实际环境中汇款,你给别人 100 块纸币,你自己就没有了,也没法自己造纸币。所以钱只能花一次。网上转账也是,转给别人 100 块的时候,第三方机构会在你的账户中扣掉 100 块。这 100 块同样也只能花一次。但是在没有第三方的网络系统中,电子货币就是一串代码,你可以无限复制,在转给别人 100 块之后,还可以自己留着,再转给其他人。这个就是通常所说的 “ 双花问题 ” ,也是比特币网络系统需要去解决的问题。
Hash :哈希算法、散列算法。简单理解就是一个运算上不可逆的函数(理论上函数都是可逆的),正向推出结果很容易,但是反向推出结果却很难。
proof-of-work :工作量证明。简单理解就是谁的算力更强,谁就有更大的概率来记录这笔交易。而这个工作量证明也是基于哈希算法的,算力所做的工作就是进行哈希碰撞,反推出合适的值。
timestamp :时间戳。记录交易发生的时间,每笔交易明细都有该笔交易的时间。交易时间也是利用哈希算法加上的。每笔交易按照时间先后顺序形成一个交易记录的链,记录这些交易之前必须完成哈希算法的工作量证明。交易记录形成以后,想要篡改,必须重新完成一次工作量证明,而这基本上很难实现。这句话比较抽象,后面的章节中还会有更详细的解释,现有一个基本的印象和框架性理解即可。
3 、电子货币 / 虚拟货币 / 数字货币 / 传统的 P2P / 去中心化 P2P :
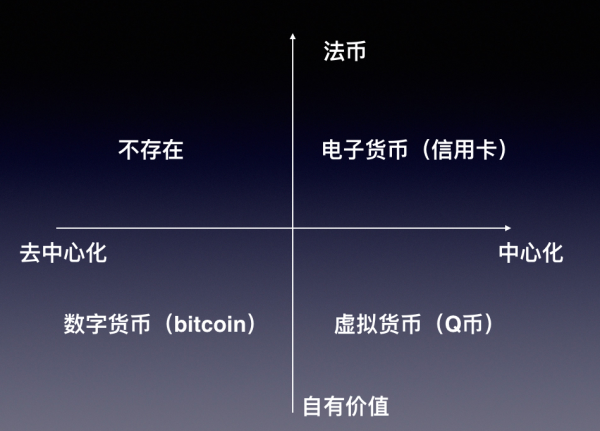
电子货币:
- 是中心化的法币,基于国家信用和税收背书的价值,不同法币之间可以依据汇率相互兑换。
- 商务印书馆《英汉证券投资词典》解释:电子货币英语为:e-money ;digital money ;e-cash ;e-currency ;electronic cash ;electronic money ;electronic wallet 。可以在互联网上或通过其他电子通信方式进行支付的手段。这种货币没有物理形态,为持有者的金融信用。随着互联网的高速发展,这种支付办法越来越流行。
- 如微信支付和支付宝支付等。
虚拟货币:
- 是指非真实的货币,如企业发行的虚拟币。
- 是中心化的自有价值币,只可以利用法币去买,不能反过来兑换为法币。
- 如 Q 币和网络游戏中使用的货币等。
数字货币:
- 是去中心化的自有价值币,可以利用法币交易和买卖。
- 数字货币简称为 DIGICCY ,是英文 “ Digital Currency ”(数字货币)的缩写。
- 数字货币不同于虚拟世界中的虚拟货币,因为它能被用于真实的商品和服务交易,而不局限在网络游戏中。早期的数码货币(数字黄金货币)是一种以黄金重量命名的电子货币形式。现在的数码货币是依靠校验和密码技术来创建、发行和流通的电子货币。其特点是运用 P2P 对等网络技术来发行、管理和流通货币,理论上避免了官僚机构的审批,让每个人都有权发行货币。
- 本文中提及的电子货币实际应理解为数字货币。
- 如比特币和莱特币等。
传统的 P2P :如 P2P 借贷、P2P 下载等。这些 P2P 都是有一个第三方和中心化的存在,借贷需要一个网上平台,下载需要迅雷这样的工具,这种 P2P 依然是中心化的。
去中心化 P2P :比特币的系统就是一个没有第三方和中心化机构的 P2P 。
4 、总结:
节点( nodes )可以随时离开和重新加入网络,这个自由进出的机制也是一个很好的调节手段:有钱赚,大家都进入,慢慢每个人就赚的少了, 然后就会有人退出,每个人赚的又变多了。该系统将处于一个动态调节和动态平衡的过程之中。可以看出中本聪也深谙经济学,将市场这只看不见的手也利用在了比特币的系统中。
摘要主要说了三件事:
- 比特币系统没有第三方依然可以被信任,并且能够避免双重支付问题;
- 这个系统并不会被攻击,是非常安全的;
- 这个系统并不复杂,架构也很简单。
1. Introduction
Commerce on the Internet has come to rely almost exclusively on financial institutions serving as trusted third parties to process electronic payments. While the system works well enough for most transactions, it still suffers from the inherent weaknesses of the trust based model. Completely non-reversible transactions are not really possible, since financial institutions cannot avoid mediating disputes. The cost of mediation increases transaction costs, limiting the minimum practical transaction size and cutting off the possibility for small casual transactions, and there is a broader cost in the loss of ability to make non-reversible payments for nonreversible services. With the possibility of reversal, the need for trust spreads. Merchants must be wary of their customers, hassling them for more information than they would otherwise need. A certain percentage of fraud is accepted as unavoidable. These costs and payment uncertainties can be avoided in person by using physical currency, but no mechanism exists to make payments over a communications channel without a trusted party.
1. 简介
互联网上的贸易,几乎都需要借助金融机构作为可资信赖的第三方来处理电子支付信息。虽然这类系统在绝大多数情况下都运作良好,但是这类系统仍然内生性地受制于 “ 基于信任的模式 ”( trust based model )固有缺陷的影响。我们无法实现完全不可逆的交易,因为金融机构总是不可避免地会出面协调争端。调解成本会增加交易的成本,并且限制了实际可行的最小交易规模,也限制了日常的小额支付交易。并且更广泛的损失还在于,很多商品和服务本身是无法退货的,如果缺乏不可逆的支付手段,互联网的贸易就大大受限。因为有潜在退款的可能,对信任的需求(或成本)就会增加。商家也必须提防自己的客户,因此会向客户索取完全不必要的个人信息。一定比例的欺诈被认为是不可避免的。而在使用物理现金的情况下,这些销售费用和支付问题上的不确定性却是可以避免的,但是没有机制可以在没有可信第三方的情况下通过通信渠道进行支付。
注解:
1 、electronic payments :
文中的 electronic payments(电子支付)在比特币网络中就可以理解为 transactions(交易),或者更准确的就是指转账行为。不过不管是在银行还是在比特币网络中,只负责记账,并不会关注你们的交付环节(广义上的交易)。就好像买卖双方经过讨价还价一番拉锯之后终于成交,只会记录买家是否给卖家转账。至于转账之前发生了什么,和银行或者比特币网络没有关系。
2 、trust based model :
基于信任的模式可以理解为基于法币信任的模式。文中没有提及这个模式的固有缺陷是什么,不过我们都知道是通货膨胀。中本聪也在比特币网络的创世区块中,不忘调侃一下法币体系,将当天的泰晤士报头版文章标题写进区块,无法篡改和删除。
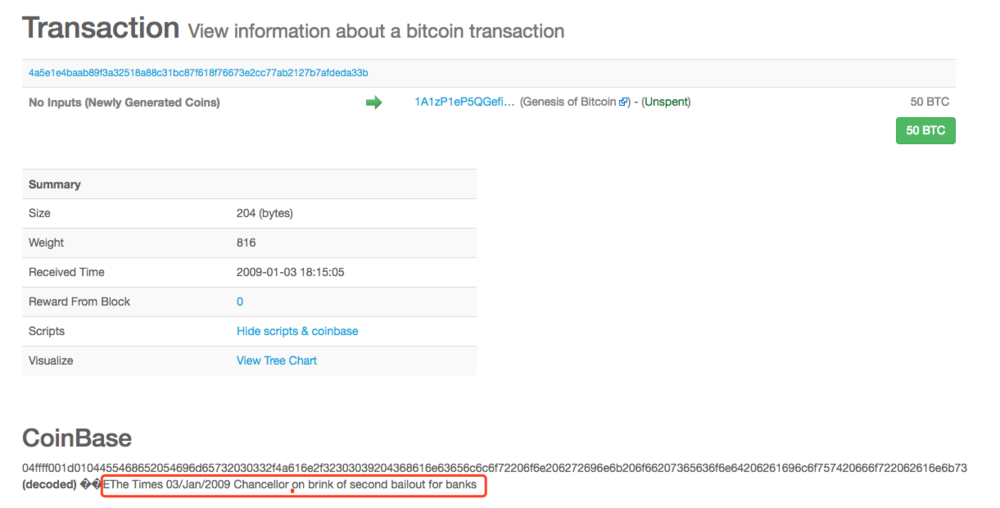
法币基于政府的信任背书,政府手中握有印钞大权,只要开足马力印钱甚至直接在银行系统上加几个 0 ,就可以无形无痛感地从所有人中掠夺财富。我们手里的钱不知不觉就贬值了,回想 2008 年之后中国投放 4 万亿 RMB ,除了火车票以外所有东西都涨价了。
3 、不可逆交易的重要性:
银行系统的转账并不是不可逆的,因为银行作为第三方机构还会受到政府、法律各方面的管辖和约束,会对一些 “ 不正常 ” 的交易或者账户采取冻结、封卡、追回等措施。可能你会问:这样不是挺好的吗?很有安全感啊,钱被骗走了或者转错了说不定还能追回来。且看中本聪是怎么分析这个问题的:
The cost of mediation increases transaction costs, limiting the minimum practical transaction size and cutting off the possibility for small casual transactions, and there is a broader cost in the loss of ability to make non-reversible payments for nonreversible services.
调解成本会增加交易的成本,并且限制了实际可行的最小交易规模,也限制了日常的小额支付交易。并且更广泛的损失还在于,很多商品和服务本身是无法退货的,如果缺乏不可逆的支付手段,互联网的贸易就大大受限。
中本聪一句话阐释了可逆转账系统的三个缺点:
- 增加整个系统的成本;
- 对一些小额转账很不划算;
- 最重要的,一些不可逆的服务无法享受对应的不可逆的支付和转账。
关于第一个缺点:对于一个需要时刻调解的转账系统,整个系统成本肯定会增加。比如会配备反洗钱人员、相关监控的硬件和软件,这些成本最终都会摊派到每个用户。
关于第二个缺点:银行转账是需要手续费的,这就对一些小额转账很不友好了,很有可能手续费就占了转账金额不可忽略的一部分。你可能会说现在转账好像都已经免费了,看看下面这张图:
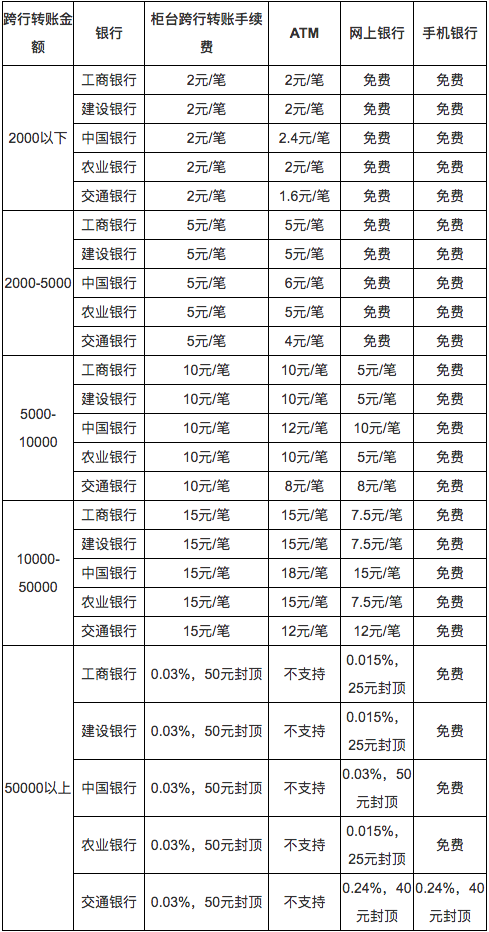
关于第三个缺点:相信很多乙方同学都能够感同身受。乙方给甲方提供的服务是不可逆的,乙方肯定想要一个同样不可逆的转账系统,干多少活给多少钱。但现状是乙方可能最后忙了很久,甲方在心领神会了你的方案之后说不满意拒绝付款或者要求退款,然后拿着你的方案为自己服务了。你作为乙方想不想手撕甲方?
4 、一定比例的欺诈被认为是不可避免的:
所以在实际的商业行为中,相关损失视作销售成本处理。
What is needed is an electronic payment system based on cryptographic proof instead of trust, allowing any two willing parties to transact directly with each other without the need for a trusted third party. Transactions that are computationally impractical to reverse would protect sellers from fraud, and routine escrow mechanisms could easily be implemented to protect buyers. In this paper, we propose a solution to the double-spending problem using a peer-to-peer distributed timestamp server to generate computational proof of the chronological order of transactions. The system is secure as long as honest nodes collectively control more CPU power than any cooperating group of attacker nodes.
所以,我们非常需要这样一种电子支付系统,它基于密码学原理而不是基于信任,使得任何达成一致的双方能够直接进行支付,从而不需要第三方中介的参与。从算力角度来说无法回滚( reverse )的交易将保护卖方免受欺诈;设立常规的第三方担保机制来保护买方也可谓非常简单。在这篇论文中,我们( we )将提出一种解决方案,通过使用点对点的分布式时间戳服务器来生成依照时间前后排列的电子交易证明,从而解决双重支付问题。只要诚实(或可信)的节点所控制的计算能力的总和,大于有合作关系的( cooperating )攻击者的计算能力的总和,那么这个系统就是安全的。
注解:
1 、为什么比特币系统比银行更值得信任?
因为比特币背后是利用的密码学原理,而密码学的背后是数学。如果说这个世界上唯一值得无条件信任的是什么,那答案就是数学了。而银行背后是什么呢?是政府、法律、公司,而这些的背后都是人。人的心理和行为都是不确定的,总会有纰漏的可能。但是数学作为世界底层逻辑的存在,是非常可靠的。如需了解比特币背后的非对称加密原理,请点击这里。
2 、比特币如何保护卖方和买方?
保护卖方很好理解,买方只要转账就不可逆转。值得注意的是现实中银行也可能把卖方给坑了,如果你想转账给别人,可是这时银行系统故障或者被攻击,你的账户钱已经扣掉,但是对方账户里的钱并没有增加,并且转账记录也没有,那你转出去的这笔钱能不能追的回来就很难说了。
常规的第三方担保机制也可以很好的保护买方。比如淘宝上的支付宝托管,买家确认收货之后,钱才从托管的账户中打入卖家账户。不过这种托管也需要借助到第三方,那么不需要第三方怎么实现呢?这个时候智能合约就可以大显身手了,这也是以太坊的主要功能。
3 、总结:
本文 “ 简介 ” 这一章,中本聪主要说明了以下五个观点:
- 现实中借助第三方机构无法实现完全不可逆的交易;
- 可逆交易存在的缺点;
- 比特币系统利用数学加密原理在没有第三方情况下实现不可逆的交易;
- 利用点对点的分布式时间戳服务器解决双重支付问题;
- 只要好算力比坏算力多,系统就是安全的。
2. Transactions
We define an electronic coin as a chain of digital signatures. Each owner transfers the coin to the next by digitally signing a hash of the previous transaction and the public key of the next owner and adding these to the end of the coin. A payee can verify the signatures to verify the chain of ownership.
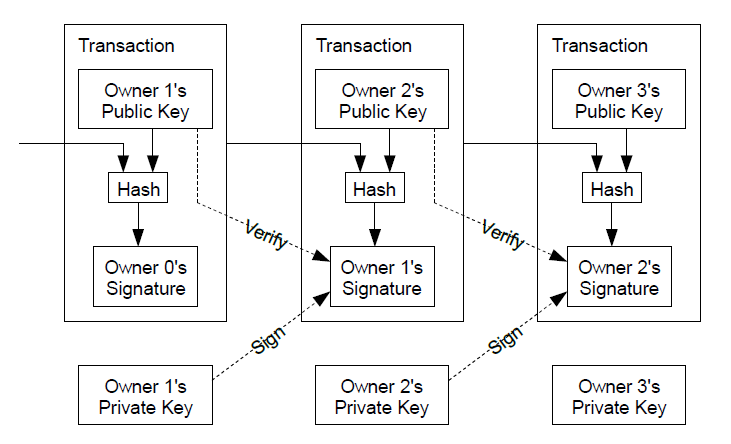
2. 交易或转账( Transactions )
我们定义一枚电子货币( an electronic coin )是这样的一串数字签名:每一位所有者(或每个持有比特币的人)在将电子货币转账给下一位所有者时,需要对上一笔交易的散列值和下一位所有者的公钥( Public key ,也就是转账对象的公钥)进行数字签名,并将这个签名附加在这枚电子货币的末尾。而收款人通过对签名进行检验,就能够验证这一串交易中比特币的归属。
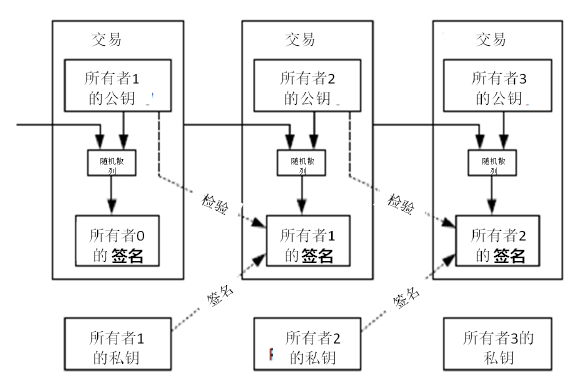
注解:
1 、数字签名在比特币交易( transaction )中的详解:
如上图所示,所有者 0 转账给所有者 1(上图左边那个 transaction ),所有者 1 再转账给所有者 2(上图中间那个 transaction )。对于所有者 1 转账给所有者 2 来说:
- 上一笔交易(所有者 0 转账给所有者 1 )的散列值和收款人所有者 2 的公钥一起进行散列运算得到所有者 1 的签名;
- 所有者 1 的签名是由所有者 1 的私钥进行签名操作得到的;
- 如需验证所有者 1 的签名需要使用所有者 1 的公钥;
- 所有者 1 将自己的签名附在交易中以后,这笔电子货币的所有权就从所有者 1 转给了所有者 2 ,并且全网公开确认。
2 、几个有关于数字签名的基础结论:
- 公钥可以推出私钥,反之不行;
- 同一套公钥和私钥之间可以相互加解密,例如公钥加密、私钥解密,和私钥加密、公钥解密;
- 私钥就代表了所有权的归属,私钥很重要,一定不要外泄(因为在转账的时候,需要用到私钥签名,谁有私钥,谁就能用这笔钱;银行卡还需要账号和密码才能取钱,但是在区块链里,只要私钥就可以了,地址都不用)。
3 、总结:
通过对这一段的阅读我们可以知道:数字签名可以确认付款人和收款人的身份,但依旧不能在没有第三方的情况下解决双重支付的问题。
The problem of course is the payee can’t verify that one of the owners did not double-spend the coin. A common solution is to introduce a trusted central authority, or mint, that checks every transaction for double spending. After each transaction, the coin must be returned to the mint to issue a new coin, and only coins issued directly from the mint are trusted not to be double-spent. The problem with this solution is that the fate of the entire money system depends on the company running the mint, with every transaction having to go through them, just like a bank.
该过程的问题在于,收款人将难以检验之前的某位所有者是否对这枚电子货币进行了双重支付。通常的解决方案( common 暗示作者并不同意)就是引入信得过的第三方权威,比如类似于造币厂( mint )的机构,来对每一笔交易进行检验,以防止双重支付。在每一笔交易结束后,这枚电子货币就要被造币厂回收,然后造币厂将发行一枚新的电子货币;而只有造币厂直接发行的电子货币才算作有效,这样就能够防止双重支付。可是该解决方案的问题在于,整个货币系统的命运完全依赖于运作造币厂的公司,每笔交易都必须通过它们,就像银行一样。
注解:
1 、哪些机构类似于造币厂?
如现实中的银行或者支付宝转账,在查看转账记录的时候,都可以清晰查到钱一旦转出,自己账户中的金额就变少了。而对于电子货币来说,需要 “ 在每一笔交易结束后,这枚电子货币就要被造币厂回收,然后造币厂将发行一枚新的电子货币 ” 来防止双重支付,可想而知这种方法有多么的原始,效率多么的低下。
2 、这里提到了铸币厂和硬币,插一个关于牛顿的故事
牛顿作为现代科学的奠基人,除了牛顿三定律和其他物理、数学成就之外,晚年还担任过英国铸币局督办(仅次于局长)后升任为局长,解决了英国 ” 劣币驱逐良币 “ 的问题。并因此被当时的安妮女王册封为骑士爵位(牛顿爵位的获得竟然不是因为他的科学成就)。
当时英国的硬币用银来铸造,一些不法分子把硬币周围剪下薄薄的一层,然后打磨光滑并继续使用, 普通人根本发现不出来(这个是不是有点像双重支付,一枚硬币剪下一部分,然后继续使用)。后来市场上流通的这种劣币越来越多,你不使用劣币就亏了,劣币驱逐良币。
最后牛顿凭借自己超越时代的科学思维方法,想出了一个绝佳的办法。以后发的硬币的周围都打上一圈锯齿,这还不够,在锯齿上还镶刻了复杂的花纹。这样防伪的功能就更强了。拿起一个你手边的硬币看看,是不是周围都会有一圈锯齿?边缘还有一些花纹?这都是牛顿的贡献 。
牛顿通过硬币边缘锯齿和花纹的方案帮助中央权威解决了双重支付的问题,而中本聪想解决的是没有第三方参与的双重支付问题。
We need a way for the payee to know that the previous owners did not sign any earlier transactions. For our purposes, the earliest transaction is the one that counts, so we don’t care about later attempts to double-spend. The only way to confirm the absence of a transaction is to be aware of all transactions. In the mint based model, the mint was aware of all transactions and decided which arrived first. To accomplish this without a trusted party, transactions must be publicly announced [1], and we need a system for participants to agree on a single history of the order in which they were received. The payee needs proof that at the time of each transaction, the majority of nodes agreed it was the first received.
我们需要收款人有某种方法,能够确保之前的所有者没有对更早发生的交易实施签名(即不会双重支付)。为了达到目的,实际上我们只需要关注本交易之前发生的交易,而不需要关注这笔交易发生之后是否会有双重支付的尝试。为了确保某一次交易是不存在的,那么唯一的方法就是获悉之前发生过的所有交易。在造币厂模型里面,造币厂获悉所有的交易,并且决定了交易完成的先后顺序。为了在不借助可信第三方的情况下达成这个目的,那么(所有)交易信息就应当被公开宣布( publicly announced )[1] ,我们需要整个系统内的所有参与者都有唯一公认的历史交易序列。收款人需要确保在交易期间绝大多数的节点都认同该交易是首次出现的。
注解:
1 、收款人如何确保在交易期间绝大多数的节点都认同该交易是首次出现的呢?
参见下一章 “ 时间戳服务器 ” 。
2 、总结:
本文 “ 交易或转账 ” 这一章,主要讲了以下几点:
- 比特币网络是怎么样转账的,如何利用数字签名来确认身份;
- 传统交易需要中央权威控制每一笔交易来防止双重支付;
- 在没有第三方的情况下,如何利用全网公开交易的方式来防止双重支付。
3. Timestamp Server
The solution we propose begins with a timestamp server. A timestamp server works by taking a hash of a block of items to be timestamped and widely publishing the hash, such as in a newspaper or Usenet post [2-5]. The timestamp proves that the data must have existed at the time, obviously, in order to get into the hash. Each timestamp includes the previous timestamp in its hash, forming a chain, with each additional timestamp reinforcing the ones before it.
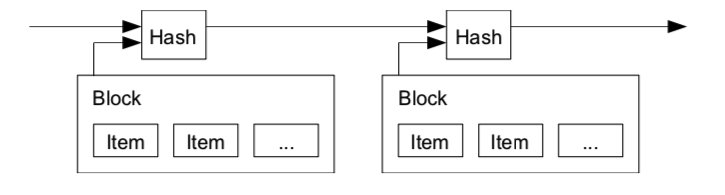
3. 时间戳服务器( Timestamp Server )
本解决方案首先提出一个 “ 时间戳服务器 ” 。时间戳服务器通过对以区块( block )形式存在的一组数据实施散列运算并加上时间戳,然后将该散列值进行广播,就像报纸或在世界性新闻组网络( Usenet )的发帖一样 [2][3][4][5] 。显然,该时间戳能够证实特定数据必然于某特定时间内是的确存在的,因为只有在该时刻存在了才能获取相应的散列值。每个时间戳应当将前一个时间戳纳入其散列值中,每一个随后的时间戳都对之前的一个时间戳进行增强( reinforcing ),这样就形成了一个链条( Chain )。
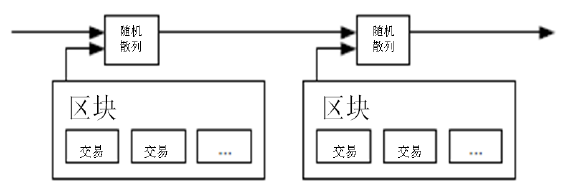
注解:
1 、什么是存在证明?
在白皮书中,时间戳是将区块中的交易进行散列运算并把这个散列值广播出去,代表这些交易是真实存在的。并没有特别强调交易是在几点几分几秒发生的。时间戳更重要的是强调交易确实发生过,是一种存在证明。因为时间戳本质上是一种存在证明,不妨先来理解一下什么是存在证明。
简单来说,存在证明就是向第三方证明某件物或事,在过去的某个时候存在或发生过。Something ever existed or happened. 就像你要向法官证明嫌疑人确实杀人了,那么你就需要拿出证据去证明这件事情确实发生过。录音也能证明你确实说了什么话。谁检举谁证明,这个就是之前币圈两个大佬争论的 “ 举证责任 ” 。
拿原文中中本聪用的报纸的例子来解释一下,为什么报纸可以作为存在证明呢?不知道你有没有过在网上买车险或者报案的体验。保险公司可能需要你将你的车和一张当天的报纸合照,报纸需要明确的显示日期,然后凭借这个照片来验车。

这样做可以确保照片中显示的车况是真实的,防止利用之前车况的照片来骗保。报纸在照片中就是时间的参照物,并且是很好的参照物:
- 报纸(新闻)不可伪造,无法预知未来、无法知道明天的上证指数,今天无法把后天的报纸印出来;
- 报纸(新闻)已经大面积的传播和公开,无法销毁和篡改了(当一件事被多数人知道了以后,想抹去这些记忆是不可能的);
- 具有明显的时间特征,报纸头版都会看到日期、天气等信息。
想要完成存在证明,必须依赖一个强有力的证据链,并且无法伪造、或者销毁、或者伪造的成本高到无法接受。比特币的时间戳和报纸发行很类似,都满足这个存在证明的条件。
2 、如何篡改区块?
如果要篡改一个区块的话,就需要把这个区块后面的所有区块都要改掉,而这个工作量是很难实现的,具体详见下一章 “ 工作量证明机制 ” 。
3 、总结:
本文 “ 时间戳服务器 ” 这一章,主要讲了以下几点:
- 时间戳是一种类似于报纸发行的存在证明机制,将每一个区块的散列值进行全网广播,并且以此形成一条由大多数节点接受的区块串连出来的链就是打时间戳了;
- 有了这些被大多数节点接受的区块串连出来的链,就可以证明这些区块里的交易确实存在,并且没有双重支付。
4. Proof-of-Work
To implement a distributed timestamp server on a peer-to-peer basis, we will need to use a proof-of-work system similar to Adam Back’s Hashcash [6], rather than newspaper or Usenet posts. The proof-of-work involves scanning for a value that when hashed, such as with SHA-256, the hash begins with a number of zero bits. The average work required is exponential in the number of zero bits required and can be verified by executing a single hash.
4. 工作量证明机制( Proof-of-Work )
为了在点对点(网络)的基础上构建一组分布式的时间戳服务器,仅仅像报纸或在世界性新闻组网络的发帖一样工作是不够的,我们还需要一个类似于亚当 • 柏克( Adam Back )提出的哈希现金( Hashcash )[6] 。在进行散列运算时,工作量证明机制引入了对某一个特定值的扫描工作,比方说在 SHA-256 下,散列值以一个或多个 0 开始。那么随着 0 的数目的上升,找到这个解所需要的工作量将呈指数增长,而对结果进行检验则仅需要一次散列运算。
注解:
1 、什么是工作量证明机制?
工作量是为了实现时间戳服务而引入的,中本聪的灵感来源于 Adam 之前发明的哈希现金,这个在参考文献里面也提到了。不过哈希现金最后并没有成功,中本聪取百家之长,其中工作量证明就来源于哈希现金。
如下图所示,在第 531857 个区块,要求区块散列值前面 18 位都是 0(最开始创世区块的要求是前面需要有 8 个 0 ):
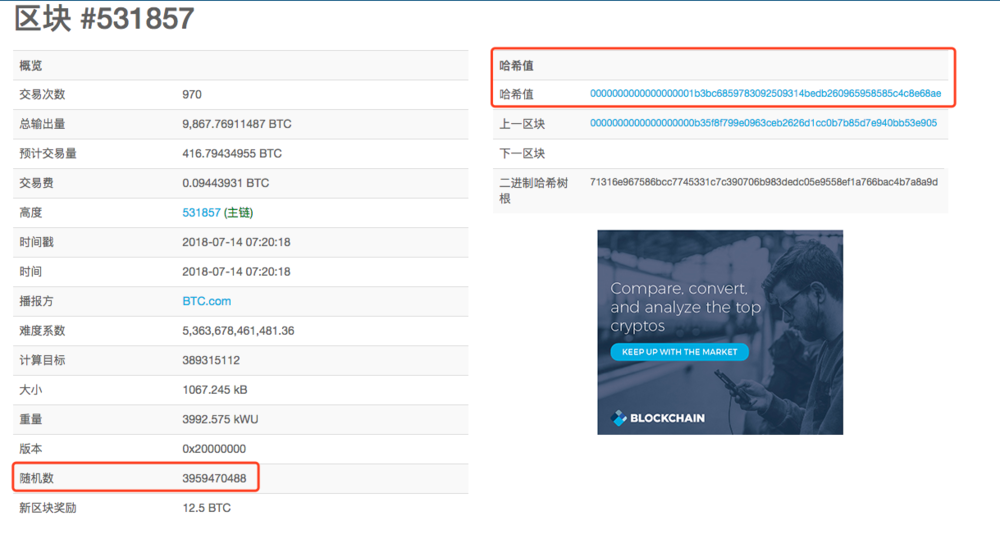
SHA-256 是由 256 位二进制的数字( 0 和 1 )构成,在散列值中转换成 64 位 16 进制的数,比如:
6b88c087247aa2f07ee1c5956b8e1a9f4c7f892a70e324f1bb3d161e05ca107b
4 位二进制的数字( 0 和 1 )一共有 2 的 4 次方也就是 16 种可能,分别对应一个 16 进制的数( a – f & 0 – 9 )。
同理还有安全性更高的 SHA-512 算法,由 512 位二进制数字构成,在散列值中转换成 128 位 16 进制的数,比如:
| d41a211567fb060fb87623e5a599508705a6c9ae7c72ff165ec1082ce2ad4a891ae428c2ceb7fca22dae803a6d2785d4c972937d0013407636f91b32e68006de |
For our timestamp network, we implement the proof-of-work by incrementing a nonce in the block until a value is found that gives the block’s hash the required zero bits. Once the CPU effort has been expended to make it satisfy the proof-of-work, the block cannot be changed without redoing the work. As later blocks are chained after it, the work to change the block would include redoing all the blocks after it.
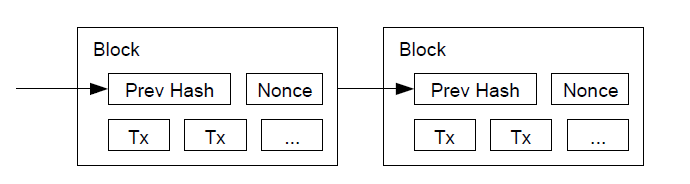
在我们的时间戳网络中,我们在区块中补增一个随机数( Nonce ),这个随机数要使得该给定区块的散列值出现了所需的那么多个 0 。我们通过反复尝试来找到这个随机数,直到找到为止,这样我们就构建了一个工作量证明机制。只要该 CPU 耗费的工作量能够满足该工作量证明机制,那么除非重新完成相当的工作量,否则该区块的信息就不可更改。由于之后的区块是链接在该区块之后的,所以想要更改该区块中的信息就还需要重新完成之后所有区块的全部工作量。
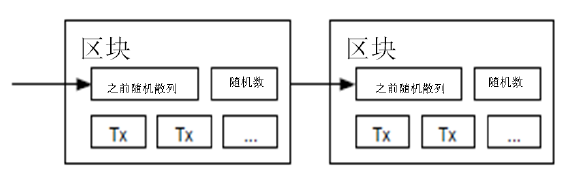
注解:
1 、使用随机数来生成散列值的过程:
如上图所示,每一个区块作散列运算的时候,包含了前一个区块的散列值、随机数和区块内的交易信息。当改动某个区块的一点点信息,都需要对这个区块后面的所有区块进行改动,这个运算量是非常大的。
The proof-of-work also solves the problem of determining representation in majority decision making. If the majority were based on one-IP-address-one-vote, it could be subverted by anyone able to allocate many IPs. Proof-of-work is essentially one-CPU-one-vote. The majority decision is represented by the longest chain, which has the greatest proof-of-work effort invested in it. If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains. To modify a past block, an attacker would have to redo the proof-of-work of the block and all blocks after it and then catch up with and surpass the work of the honest nodes. We will show later that the probability of a slower attacker catching up diminishes exponentially as subsequent blocks are added.
该工作量证明机制还解决了在集体投票表决时谁是大多数的问题。如果决定大多数的方式是基于 IP 地址,即一 IP 地址一票,那么如果有人拥有分配大量 IP 地址的权力,则该机制就被破坏了。而工作量证明机制的本质则是一 CPU 一票。“ 大多数 ” 的决定表达为最长的链,因为最长的链包含了最大的工作量。如果大多数的 CPU 为诚实(或可信)的节点控制,那么诚实(或可信)的链条将以最快的速度延长,并超越其他的竞争链条。如果想要对已出现的区块进行修改,攻击者必须重新完成该区块的工作量外加该区块之后所有区块的工作量,并最终赶上和超越诚实(或可信)节点的工作量。我们将在后文说明,随着后续块的添加,一个较慢的攻击者试图赶上的概率将呈指数级递减。
注解:
1 、一 CPU 一票是否公平?
中本聪在写这篇论文的时候可能认为只要一 CPU 一票,就不会出现一个人拥有很多 CPU 的情况。每个人一台电脑,能够实现去中心化的算力分布。但是他没有想到后来会出现专门针对比特币的矿机,导致普通电脑几乎不可能完成比特币的工作量证明。
但只要大多数的节点是好的,那么最长的链条也就是好的。想篡改数据的节点由于算力不够,无法超越诚实(或可信)节点的链条成为最长的链条,所以还是安全的。只有想篡改数据的节点的算力超过了全网算力的 50 % ,才有可能篡改成功。
To compensate for increasing hardware speed and varying interest in running nodes over time, the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour. If they’re generated too fast, the difficulty increases.
随着时间的推移,硬件的运算速度在高速增长,同时节点参与网络的程度也会有所起伏;为了补偿(或解决)这些问题,工作量证明的难度( the proof-of-work difficulty )会根据每小时生成区块的平均速度来做相应的调整。如果区块生成的速度过快,那么难度就会提高。
注解:
1 、如何动态调节工作量证明的难度?
中本聪考虑到了摩尔定律,即未来的算力肯定越来越强,也考虑到了矿工的数量可能也在不停地变化,这些都会导致全网的算力造成波动。所以完成工作量证明的难度也会调整,以保证每个小时生成的区块数量是差不多的。
现在每个小时差不多生成 6 个区块,而想要调整工作量证明的难度也很简单,只需要调整每个区块的散列值前面有 N 位都是 0 的条件就可以了。N 越大,散列值前面都是 0 的位数就越多,找到的概率就越小,随机数就越难找,难度就越大;反之亦然。
工作量证明目前也被认为是最安全的共识机制,因为没能力(算力不够)的人无法作恶,而有能力的(算力足够)人却是最维护这个系统的人,最不允许让人来作恶的。世界上并不存在绝对安全,信息安全也是一样。比特币系统是通过对作恶成本的增加使得作恶的收益还不如按照规则行事。
我们俗称的 “ 挖矿 ” ,其实就是矿机在不停地找寻随机数( nonce ),使得区块的散列值前面 N 位是 0 。
让我们来看看比特币诞生以来的挖矿难度变化:

创世区块:区块散列值前 8 位是 0(创世区块前面虽然有 10 个 0 ,但要求是 8 个 0 ;在算到前面 8 位是 0 时,碰巧前面 10 位都是 0 ,可以看到下一区块就是 8 个 0 )。

区块 #100000 :区块散列值前 11 位是 0 。

区块 #200000 :区块散列值前 13 位是 0 。
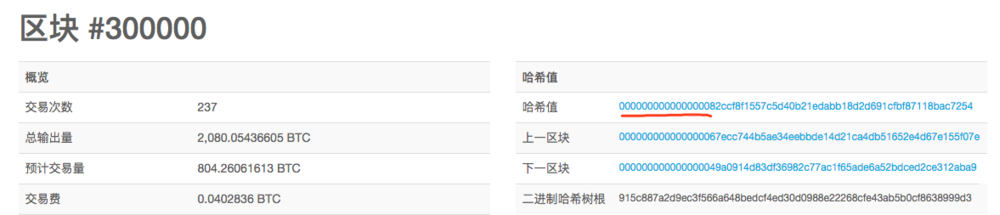
区块 #300000 :区块散列值前 16 位是 0 。
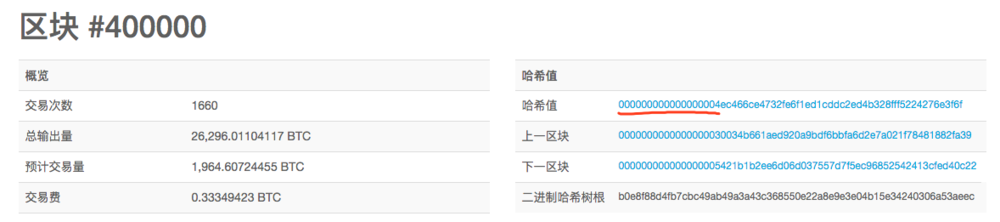
区块 #400000 :区块散列值前 17 位是 0 。

区块 #531857 :区块散列值前 18 位是 0 。
散列值前面 0 的位数一直在增加,挖矿难度(寻找符合条件的随机数)也在呈指数级上涨。如果你想体验一下这种难度,不妨在自己的名字后面加数字(如张三1 、张三2 … 张三199 … ),感受一下生成的散列值前面有 1 个 0 、2 个 0 、3 个 0 的难度(体验网址:Hash: online hash value calculator )。相信你挨个试的话,很快就放弃了;如果你会编程,相信你也能体会到其中难度巨大的差别。
2 、总结:
本文 “ 工作量证明机制 ” 这一章,主要讲了以下几点:
- “ 挖矿 ” 是什么?(或什么是工作量证明机制?)寻找随机数,让区块散列值的前 N 位都是 0 ;
- 为什么比特币的信息很难被篡改?因为一旦篡改就牵一发而动全身,需要对改动区块以后的所有区块重新做一次工作量证明,而这个工作量是非常庞大的,没有超过全网一半以上的算力是不可能实现的;
- 为什么工作量证明保证了比特币的安全性?想做恶的人没能力(算力),有能力(算力)的人根本不想作恶,所以这能让大部分人成为既得利益者和系统安全的守护者。
5. Network
The steps to run the network are as follows:
- New transactions are broadcast to all nodes.
- Each node collects new transactions into a block.
- Each node works on finding a difficult proof-of-work for its block.
- When a node finds a proof-of-work, it broadcasts the block to all nodes.
- Nodes accept the block only if all transactions in it are valid and not already spent.
- Nodes express their acceptance of the block by working on creating the next block in the chain, using the hash of the accepted block as the previous hash.
5. 网络
在网络中运行(比特币系统)的步骤如下:
- 新的交易向全网进行广播;
- 每个节点都将收到的交易信息纳入一个区块中;
- 每个节点都尝试为自己的区块找到一个具有足够难度的工作量证明;
- 当一个节点找到了一个工作量证明,它就向全网进行广播;
- 当且仅当包含在该区块中的所有交易都是有效的且是之前未存在过的,其他节点才接受该区块;
- 节点通过在链中创建下一个块来表示对块的接受,使用接受块的散列作为前一个散列。(或节点接受一个区块的方式就是在生成下一个区块的时候,将这个区块的散列值添加到下一个区块中,从而得到下一个区块的散列值。)
Nodes always consider the longest chain to be the correct one and will keep working on extending it. If two nodes broadcast different versions of the next block simultaneously, some nodes may receive one or the other first. In that case, they work on the first one they received, but save the other branch in case it becomes longer. The tie will be broken when the next proof-of-work is found and one branch becomes longer; the nodes that were working on the other branch will then switch to the longer one.
节点始终都将最长的链条视为正确的链条,并持续工作来延长它。如果两个节点同时广播下一个区块的不同版本,那么其他节点在接收到这两个区块的时间上将存在先后之分。在这种情况下,他们将在率先收到的区块上进行工作,但也会保留另外一个链条,以防后者变成最长的链条。该僵局( tie )的打破要等到下一个工作量证明被找到且其中的一条链条成为较长的一条时,那么在另一条分支链条上工作的节点将转换阵营,开始在较长的链条上工作。
注解:
1 、丢弃的区块(以及区块中的交易信息)将如何处理?
矿工们回到最长链上之后,那个曾经被保留的区块也就被丢弃了,这个区块也被叫做孤块。区块中的交易信息将会被重新打包到区块里,进入到最长链中。
New transaction broadcasts do not necessarily need to reach all nodes. As long as they reach many nodes, they will get into a block before long. Block broadcasts are also tolerant of dropped messages. If a node does not receive a block, it will request it when it receives the next block and realizes it missed one.
所谓 “ 新的交易要广播 ” ,实际上不需要抵达全部的节点。只要交易信息能够抵达足够多的节点,那么他们将很快被整合进一个区块中。区块的广播对丢失的信息也是具有容错能力的。如果一个节点没有收到某个区块,那么在当该节点收到下一个区块并发现自己缺失了某个区块时,该节点就会提出下载该区块的请求。
注解:
1 、节点具体是如何判断自己缺失了某个区块的?
因为每一个区块之间都是通过散列值互相关联并且确定先后顺序的。如果你收到一个区块,其中包含的上个区块的散列值是你没有见过的,这个时候你就意识到你缺少了上一个区块,就会要求同步这个信息。
2 、这一章的内容比较简单,可以看做是对比特币白皮书前半部分的一个总结:
通过数字签名,可以确定一笔转账发起人的身份和付款人的确拥有需要转出的比特币。虽然确定了交易双方的所有权,但是还需要解决双重支付的问题。
在传统方案中,会借助中心化组织来解决问题,比如银行会记录每一笔转账信息。但是在去中心化的点对点网络中,解决双重支付就需要一个公开的账本,和一个网络系统来共同维护这个账本。
该账本和网络系统具有三个特点:
- 所有交易全网公开;
- 利用时间戳服务,对所有交易进行时间上的排序,形成一条交易链;
- 通过工作量证明,让矿工们利用算力来竞争获得记账的机会。
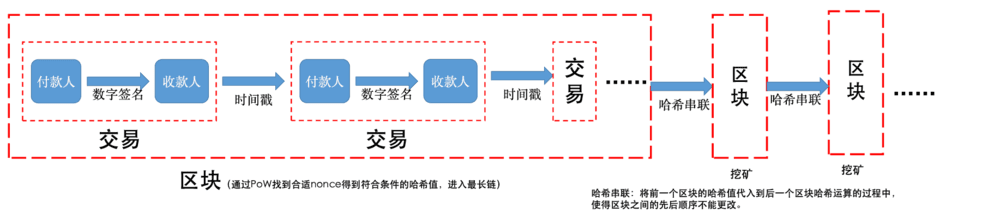
每一个网络节点都将自己收到的交易信息放到一个区块中,同时每一个节点也需要为自己打包的区块找到合适的随机数( nonce )来生成符合要求的散列值,让自己的区块进入全网接受的最长链(即挖矿)。
6. Incentive
By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block. This adds an incentive for nodes to support the network, and provides a way to initially distribute coins into circulation, since there is no central authority to issue them. The steady addition of a constant of amount of new coins is analogous to gold miners expending resources to add gold to circulation. In our case, it is CPU time and electricity that is expended.
6. 激励(或奖励)
我们约定如此:每个区块的第一笔交易是一笔特殊的交易,该交易将产生新的电子货币,这些电子货币由该区块创造者所拥有。这样就增加了节点支持该网络的动力(即通过这种激励方式让更多的节点参与进来),并在没有中央集权机构发行货币的情况下,提供了一种将电子货币分配到流通领域的方法。这种将一定数量新货币持续增添到货币系统中的方法,与耗费资源去挖掘金矿并将黄金注入到流通领域非常类似。在我们的例子中,CPU 的时间和电力消耗就是消耗的资源。
The incentive can also be funded with transaction fees. If the output value of a transaction is less than its input value, the difference is a transaction fee that is added to the incentive value of the block containing the transaction. Once a predetermined number of coins have entered circulation, the incentive can transition entirely to transaction fees and be completely inflation free.
另外一个激励的来源则是交易手续费( transaction fees )。如果某笔交易的输出值小于其输入值,那么差额就是交易手续费,该手续费将被增加到包含该笔交易的区块的激励中。只要既定数量的电子货币已经进入流通,那么激励机制就可以完全转变为依靠交易手续费来进行,并且完全没有通货膨胀。
注解:
1 、每产生一个区块,比特币会给予多少激励(或奖励)?
在比特币的生命周期中,将会有 2100 万个比特币被发行,所有的比特币均来自创建新区块时对矿工的激励。第一个创世区块的激励设定为 50 个比特币,此后每创建 21 万个区块,激励减半。激励金额在 2012 年的时候从 50 个比特币减半为 25 个比特币,2016 年从 25 个比特币减半为 12.5 个比特币。大概在 2020 年就会再减半为 6.25 个比特币。让我们一起来看一下比特币的区块链代码中关于减半算法的代码:
// validation.cpp line 1138 // v0.16 CAmount GetBlockSubsidy(int nHeight, const Consensus::Params& consensusParams) { int halvings = nHeight / consensusParams.nSubsidyHalvingInterval; // Force block reward to zero when right shift is undefined. if (halvings >= 64) return 0; CAmount nSubsidy = 50 * COIN; // Subsidy is cut in half every 210,000 blocks which will occur approximately every 4 years. nSubsidy >>= halvings; return nSubsidy; }
当区块链数量除以 210000 大于等于 64 时,激励金额直接返回 0 。
2 、比特币具体会在什么时间点完全依靠交易手续费来进行激励,以避免通货膨胀?
比特币一共有 2100 万个,现在已经挖出了 1700 万个左右,大概在 2140 年全部挖完。在那以后,比特币网络的激励机制就完全依靠比特币交易的手续费了(注意:现在的比特币交易,在某些情况下也是收取一定的手续费的,不是等到 2140 年才开始收取手续费)。比特币也实现了不增发、没有通货膨胀,同时还能激励节点继续维护这个网络的目的。
The incentive may help encourage nodes to stay honest. If a greedy attacker is able to assemble more CPU power than all the honest nodes, he would have to choose between using it to defraud people by stealing back his payments, or using it to generate new coins. He ought to find it more profitable to play by the rules, such rules that favour him with more new coins than everyone else combined, than to undermine the system and the validity of his own wealth.
激励系统也有助于鼓励节点保持诚实(或可信)。如果有一个贪婪的攻击者能够调集比所有诚实(或可信)节点加起来还要多的 CPU 计算能力,那么他将面临一个选择:要么将其用于双重支付攻击,要么将其用于产生新的电子货币。那么他应该发现,按照规则行事、诚实工作是更有利可图的。因为遵守规则使得他能够拥有更多的电子货币,而不是破坏这个系统和其自身财富的有效性。
注解:
1 、中本聪是如何保证人们不作恶的呢?
中本聪从技术和利益两个方面防止了节点作恶的可能:
- 技术方面,必须拥有全网一半以上的算力才有可能成功攻击系统;
- 利益方面,即使真的拥有一半以上的算力,那为什么不好好利用这个算力去挖出更多的比特币呢?这个收益比攻击比特币系统大多了。
拥有巨大算力的矿霸和比特币是一根绳上的蚂蚱,一旦比特币系统出问题,受影响最大的就是他们。所以矿霸不但不会去攻击系统,反而会是第一个出来保护这个系统的人。
根据经济学的基本原理:人们会对激励做出反应;如果没有反应,则说明激励机制有问题。
如果比特币网络系统( Bitcoin )没有比特币( bitcoin )作为激励的话,相信不管是 Bitcoin 还是 bitcoin 都活不到今天。从诞生到现在快十年的时间,bitcoin 经历了币价的暴涨暴跌、交易所被盗、暗网勒索等负面事件,但是比特币系统( Bitcoin )相对来说还是非常安全的( 2010 年 8 月 15 日,一名身份不明的黑客几乎摧毁了比特币,这名黑客利用比特币的一个 Bug ,在编号 74638 的区块上凭空制造了 1844.67 亿枚比特币,详情请点击这里)。
如何设计激励机制也成为了后来区块链项目必须考虑的问题,如何通过 token 让更多的项目参与者成为一个利益共同体,也是通证经济的基本思想。
2 、什么是通证经济?
通 = 流通,证 = 信任;即以区块链的技术为基础,通过经济正向激励和反向激励来实现人与人大规模的强协作。
3 、总结:
本文 “ 激励 ” 这一章,主要讲了以下几点:
- 比特币总量恒定,没有中央权威机构发行,需要投入算力资源才能获得奖励;
- 诚实的节点收益大,作恶的节点收益小、代价大;
- 所有比特币挖完之后,依然可以依靠交易手续费来获得奖励。
7. Reclaiming Disk Space
Once the latest transaction in a coin is buried under enough blocks, the spent transactions before it can be discarded to save disk space. To facilitate this without breaking the block’s hash, transactions are hashed in a Merkle Tree [7][2][5], with only the root included in the block’s hash. Old blocks can then be compacted by stubbing off branches of the tree. The interior hashes do not need to be stored.
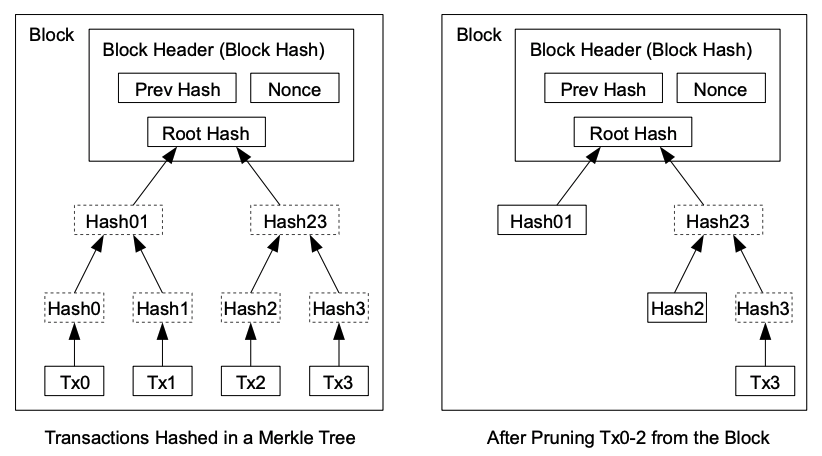
7. 回收硬盘空间
一旦货币中的最新交易被埋藏在足够的区块下,那么就可以丢弃之前的交易信息,以节约硬盘空间。为了在不破坏区块的散列值的情况下实现这一点,交易信息在散列时被构建成一种 Merkle 树( Merkle Tree )[7] 的形态,使得只有根( root )包含了区块的散列值。通过将该树( tree )的分支拔除( stubbing off )的方法,老区块就能被压缩。而内部的散列值是不必保存的。
A block header with no transactions would be about 80 bytes. If we suppose blocks are generated every 10 minutes, 80 bytes * 6 * 24 * 365 = 4.2MB per year. With computer systems typically selling with 2GB of RAM as of 2008, and Moore’s Law predicting current growth of 1.2GB per year, storage should not be a problem even if the block headers must be kept in memory.
一个不含交易信息的区块头( Block header )仅有 80 字节。如果我们设定区块生成的速率为每 10 分钟一个,那么每年产生的数据是 4.2 MB 。( 80 bytes * 6 * 24 * 365 = 4.2 MB )。2008 年计算机系统通常的内存容量为 2 GB ,根据摩尔定律的预言从现在开始(内存)每年增长 1.2 GB ,那么即使将全部的区块头存储于内存之中都不是问题。
注解:
1 、什么是默克尔树( Merkle Tree )?
这一章的核心内容就是删除不必要的交易信息,节约硬盘空间。要理解这个机制,必须弄清楚一个概念就是默克尔树( Merkle Tree )。
白皮书中的插图(如上图所示)很直观地解释了 Merkle Tree ,它是一个层层向上且归并哈希的数据结构,数据的完整性层层锁定,修改任意一个地方都会引起后续的连锁反应。
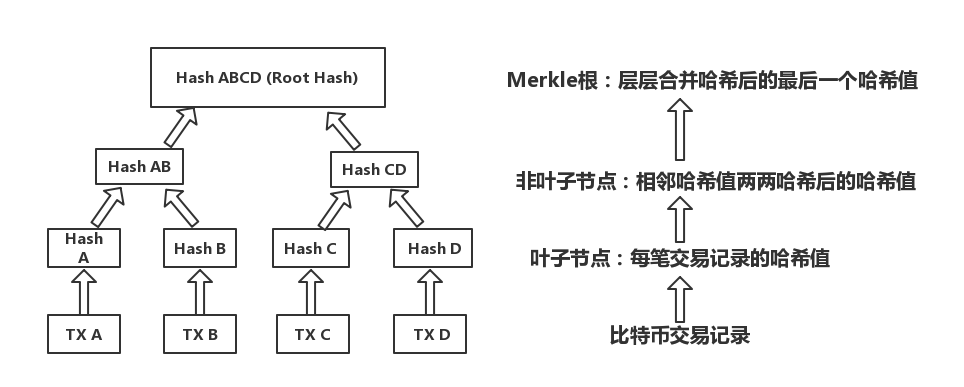
如上图所示,假设一个区块中有 4 笔交易( TX A – TX D ),首先分别对每一笔交易做一次散列运算,得到对应的散列值( Hash A – Hash D ),然后得出的散列值两两配对继续做散列运算( Hash A 和 Hash B 得到 Hash AB ,Hash C 和 Hash D 得到 Hash CD ),然后 Hash AB 和 Hash CD 两个散列值再做一次散列运算,得到根散列值( Root Hash )。只有这个根散列值被保存在区块头中,而剩下的交易信息都可以删除。这样既可以节约硬盘空间,还能够保证交易信息不被篡改(根散列值下的任意一处信息发生变化,根散列值就会变化)。
插图中一个区块只有 4 笔交易,而在实际情况中,比特币一个区块大约有 4000 笔交易,但是得出根散列值的步骤也是一样的。从 4000 多笔交易信息到 4000 多笔散列值,一直向上两两归并,计算得出根散列值。
在 2016 年以前,即使记录所有的交易记录,对于一般的 PC 来说也是可以接受的。但是随着最近几年比特币共识的迅速扩大,2018 年一个包含全部交易信息的全节点钱包已经需要 100 多 GB 的硬盘空间了,并且还在持续增加中。
虽然普通 PC 保存全部交易信息,运行全节点钱包很不现实,但是整个比特币网络依然需要一些大的节点去保存全部的交易记录。而一般用户可以用轻钱包、网络钱包,他们对存储空间要求很低。
2 、总结:
本文 “ 回收硬盘空间 ” 这一章,主要讲了:
比特币区块链的全节点数据量越来越庞大,必须使用 Merkle Tree(一个层层向上且归并哈希的数据结构,数据的完整性层层锁定,修改任意一个地方都会引起后续的连锁反应)来减少数据量,同时还保证交易数据不能被篡改。普通用户不必同步全部交易数据,使用轻钱包即可。
8. Simplified Payment Verification
It is possible to verify payments without running a full network node. A user only needs to keep a copy of the block headers of the longest proof-of-work chain, which he can get by querying network nodes until he’s convinced he has the longest chain, and obtain the Merkle branch linking the transaction to the block it’s timestamped in. He can’t check the transaction for himself, but by linking it to a place in the chain, he can see that a network node has accepted it, and blocks added after it further confirm the network has accepted it.
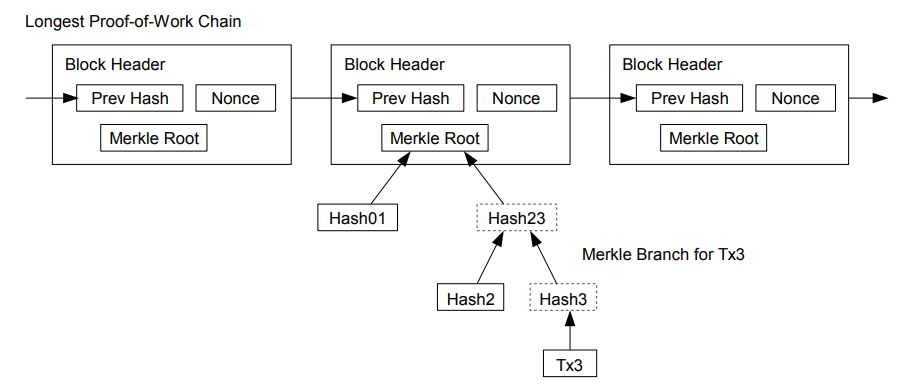
8. 简化的支付确认( Simplified Payment Verification )
在不运行完整网络节点( “ 完整网络节点 ” 可理解为 “ 存储了所有区块和所有交易信息的节点 ” )的情况下,也能够对支付进行检验。一个用户需要保留最长的工作量证明链条的区块头的拷贝,它可以不断向网络发起询问,直到它确信自己拥有最长的链条,并能够通过默克尔树的分支追溯到它被加上时间戳并纳入区块的那次交易。节点想要自行检验该交易的有效性原本是不可能的,但通过追溯到链条的某个位置,它就能看到某个节点曾经接受过它,并且于其后追加的区块也进一步证明全网曾经接受了它。
注解:
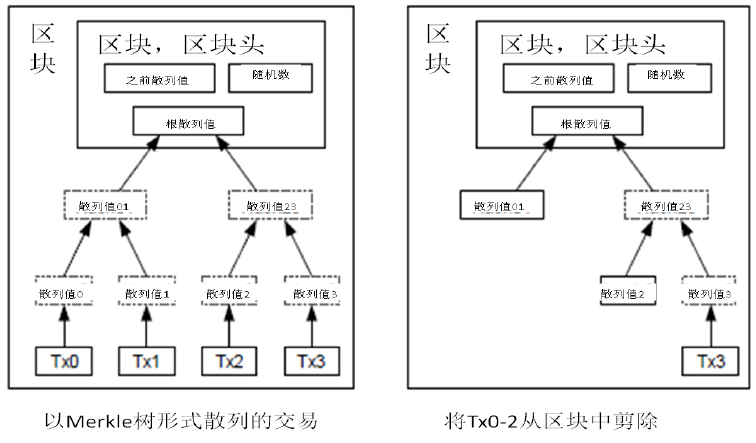
1 、在默克尔树的分支被修剪掉的情况下,如何验证某一笔交易是否有效?
如白皮书插图所示(如上图所示),如果我们需要检验 Tx3 这笔交易是否真实有效,我们只用看 Tx3 这笔交易的散列值一直往上递归到的根散列值( Merkle Root ),和已有最长链对应区块的根散列值是否一致。如果一致则证明该交易真实有效;如果不一致则证明该交易无效,因为该交易没有被其他节点承认。
As such, the verification is reliable as long as honest nodes control the network, but is more vulnerable if the network is overpowered by an attacker. While network nodes can verify transactions for themselves, the simplified method can be fooled by an attacker’s fabricated transactions for as long as the attacker can continue to overpower the network. One strategy to protect against this would be to accept alerts from network nodes when they detect an invalid block, prompting the user’s software to download the full block and alerted transactions to confirm the inconsistency. Businesses that receive frequent payments will probably still want to run their own nodes for more independent security and quicker verification.
因此,只要诚实(或可信)的节点控制了网络,该检验机制就是可靠的。但是,当全网被一个算力占优的攻击者攻击时,将变得较为脆弱。由于网络节点能够自行确认交易的有效性,所以只要攻击者能够持续地保持算力优势,这种简化的机制将会被攻击者伪造的( fabricated )交易所欺骗。那么一个可行的策略就是,只要他们发现了一个无效的区块,就立刻发出警报,收到警报的用户的软件将立刻开始下载完整的区块和被警告有问题的交易信息,以便对信息的不一致进行判定。对于日常会发生大量收付款的商业机构来说,可能仍会希望运行他们自己的完整节点(即存储了所有区块和所有交易信息的节点),以保持较大的独立安全性和检验的快速性。
注解:
1 、比特币的区块结构:
“ 简化的支付确认 ” 和上一章 “ 回收硬盘空间 ” 的内容是高度相关的,在节约硬盘空间的基础上,还要保证交易的安全和可检验。为了更好的理解比特币区块链是如何做到这一点的,我们来梳理一下比特币区块链中一个区块的结构。
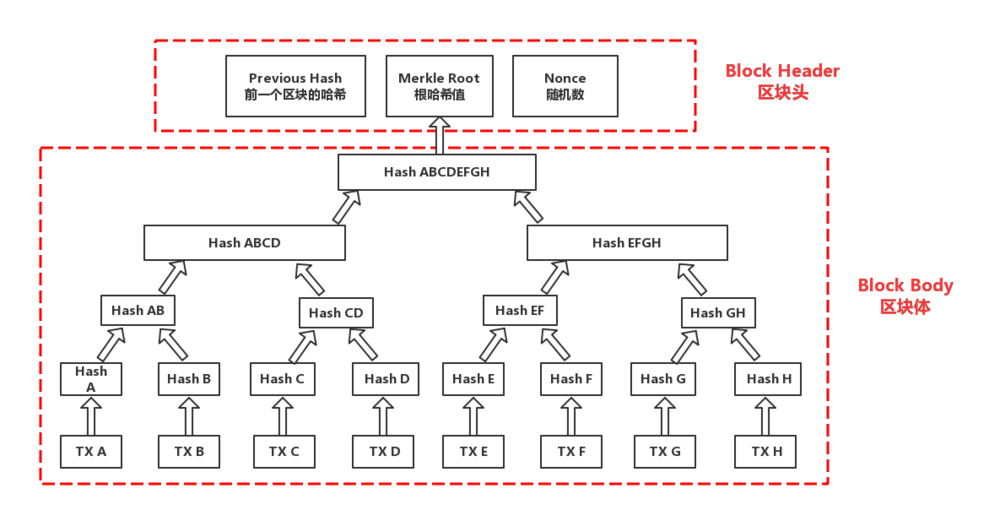
如上图所示,一个区块是由区块体( Block Header )和区块头( Block Body )两部分构成的,区块体包含着该区块内全部的交易信息,而区块头只有三个数据:
- Previous Hash :前一个区块的散列值(利用哈希串联保证区块的先后顺序,让交易无法篡改),
- Merkle Root :该区块的根散列值(该区块所有交易信息的总和),
- Nonce :随机数(在工作量证明机制下找到的、符合相关要求的数字)。
区块头包含的三个数据可以用来确定一个区块的所有信息。需要注意的是,通常所说的区块散列值,其实指的是区块头的散列值,也就是将区块头做散列运算,而并非对整个区块做散列运算,也不是区块的根散列值。区块散列值(或区块头散列值)可以唯一、明确地标识一个区块。
一个区块头的大小只有 80 个字节,而一个区块的大小在 1 M 左右,两者相差 1 万多倍。而简化的支付确认只需要下载区块头的信息,这样既节约了磁盘空间,也保证了交易的安全可靠。
9. Combining and Splitting Value
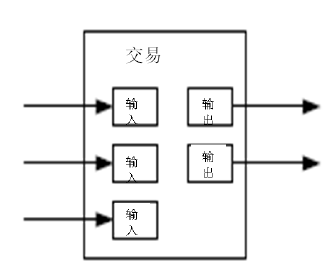
Although it would be possible to handle coins individually, it would be unwieldy to make a separate transaction for every cent in a transfer. To allow value to be split and combined, transactions contain multiple inputs and outputs. Normally there will be either a single input from a larger previous transaction or multiple inputs combining smaller amounts, and at most two outputs: one for the payment, and one returning the change, if any, back to the sender.
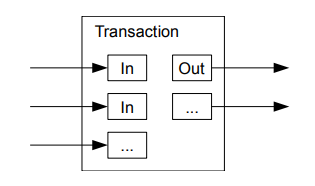
9. 价值的组合与拆分( Combining and Splitting Value )
虽然可以单个单个地对电子货币进行处理,但要在一次转账中对每一分钱进行单独的交易是不明智的。为了使得价值易于拆分与组合,交易被设计为可以包含多个输入和输出。一般而言,(一笔交易的输入可能来自)某次价值较大的前次交易构成的单一输入,或者由某几个价值较小的前次交易共同构成的并行输入,而输出最多只有两个:一个用于支付,另一个用于找零(如有)。
注解:
1 、如何理解 “ 在一次转账中对每一分钱进行单独的交易是不明智的 ” ?
这就好比手里有 10 张 1 元的纸币,去买一个 10 块钱的东西。最好的办法就是一次性直接将 10 张纸币给到卖家,而不是分 10 次交易、每次交易给 1 块钱。
2 、如何理解交易中的找零?
就好像用 100 元纸币去买 10 块钱的东西,10 块支付给卖家,90 元找零给自己。
It should be noted that fan-out, where a transaction depends on several transactions, and those transactions depend on many more, is not a problem here. There is never the need to extract a complete standalone copy of a transaction’s history.
需要指出的是,一笔交易依赖于之前的多笔交易,而这些交易又各自依赖于更多的交易,但这并不存在任何问题。因为这个工作机制并不需要展开检验之前发生的所有交易历史。
注解:
1 、为什么这个工作机制不需要展开检验之前发生的所有交易历史?
不管你现在所拥有的比特币之前的交易记录如何,矿工如何挖矿挖出(区块奖励)然后一步一步到你的手里,都不会影响你的正常使用。就好像现在我们从银行 ATM 里取出了纸币,不管这张纸币从造币厂到从 ATM 取出经历了怎样的辗转,我们都可以正常使用。
2 、什么是 UTXO( Unspent transaction output )?
这一章主要讲了比特币的面额(价值)是可以合并和分解的,可以让交易更方便,但是这一章更重要的目的是介绍比特币系统独特的记账体系,以及一个非常重要的概念 —— UTXO( Unspent transaction output )。
比特币作为一个去中心化的公开账本,和我们传统采用的 “ 余额式记账 ” 方法有很大的不同。余额记账更符合我们的直觉,而比特币的 “ 记币记账 ” 有一点反直觉。
先来看日常用得最多的余额记账方法。比如消费者 A 现在有 1000 元,出去打车花费 50 元,买衣服花费 300 元,吃饭花费 100 元,看电影花费 100 元,那么 A 的余额还剩 450 元( 1000 – 50 – 300 – 100 – 100 );同理,商家 B 有 1000 元并且经营一家餐厅,一天有 50 个顾客消费,平均每个顾客消费 100 元,那么 B 的余额就是 6000 元( 1000 + 50 * 100 )。这个就是日常使用的余额记账法,简单明了。
比特币系统的账本公开透明,矿工都有记账的权利,矿工的记账只是记录每一个地址的交易信息,而并不计算地址的余额(也就是一个地址还有多少 btc ),平时打开比特币钱包看到的余额也是钱包软件(而不是矿工)根据账户的 UTXO 而计算出来的。作为和用户直接接触的钱包界面,易用性肯定是必须考虑的问题。而我们也必须知道,比特币采取的并不是 “ 余额记账 ” ,而是 “ 记币记账 ” 。
A 最先计算出区块的随机数并生成区块,获得 12.5 个 btc 的区块奖励,那么 A 的地址现在就有 12.5 个 btc 。

如上图所示,A 得到 12.5 个 btc 的挖矿奖励之后,经过买车买房到卖车卖房和打工这些过程,现在 A 还有多少 btc 呢?这个时候只需要计算属于 A 的 UTXO(未花费出去的 btc ,即标红部分)就可以了。现在 A 一共有 24 btc ,从钱包中看到的余额,也是自动计算出来的。这个就好像清点钱包的过程,现在 A 钱包中一共有 1 张 20 btc 钞票,1 张 1.5 btc 钞票,1 张 1 btc 钞票,3 张 0.5 btc 钞票,合计 24 btc 。我们很容易想成最后汇总成 1 张 24 btc 的钞票,实际上却并不是。这个过程就是比特币价值或者面额的分割( splitting value )。
现在 A 可以利用这些零散的 UTXO(相当于零钱)而不是一张 24 btc 的整钱继续消费。比如 A 现在想买一个价值 1.5 btc 的汽车,可能会有以下三种方案:
- 直接将那个 1.5 btc 的 UTXO 支付出去;
- 将 3 个 0.5 btc 的 UTXO 支付出去;
- 将 1 个 1 btc 和 1 个 0.5 btc 的 UTXO 支付出去。
按照我们通常的想法,把零钱花出去,那么最有可能采取第二种方案了。而钱包也会采取他认为最合适的方案(可能是上述任何一种),而不会将 20 个 btc 的 UTXO 支付出去,还要再找零。这个过程就是比特币价值或者面额的合并( combining value )。
我们可以把 UTXO 想象成零钱,只不过它是可以任意数值。它静静躺在钱包里,不会自动合并,也不会自动拆分。在需要交易的时候,钱包会选择最合适的方案,尽可能不用找零或者将更多的零钱花出去。
这就是比特币价值的合并与分割,合并和分割之后成为 UTXO ,在不断合并和分割的过程中,UTXO 数量也实现了动态平衡。
10. Privacy
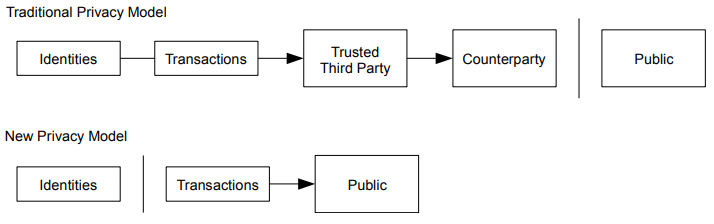
The traditional banking model achieves a level of privacy by limiting access to information to the parties involved and the trusted third party. The necessity to announce all transactions publicly precludes this method, but privacy can still be maintained by breaking the flow of information in another place: by keeping public keys anonymous. The public can see that someone is sending an amount to someone else, but without information linking the transaction to anyone. This is similar to the level of information released by stock exchanges, where the time and size of individual trades, the “tape”, is made public, but without telling who the parties were.
10. 隐私( Privacy )
传统的银行模式实现了一定程度的隐私保护,交易的相关方和可信任的第三方对交易信息的索取是严格受限的。将交易信息向全网进行广播,就意味着这样的方法失效了,但是仍然可以通过打破另一个地方的信息流( “ 打破另一个地方的信息流 ” 可理解为 “ 另一种方式 ” )来保护隐私:将公钥保持为匿名。公众得知的信息仅仅是某个人将一定数量的电子货币发给了另外一个人,但是难以将该交易信息同特定的人联系在一起(也就是说,公众难以知晓这些人究竟是谁)。这同股票交易所发布的信息是类似的,股票交易发生的时间和交易量是记录在案( the “tape” )且可供查询的,但是交易双方的身份信息却不予透露。
注解:
1 、如何理解 “ 公众得知的信息仅仅是某个人将一定数量的电子货币发给了另外一个人,但是难以将该交易信息同特定的人联系在一起 ” ?
因为只能看到比特币在 “ 乱码 ” 地址之间进行转账,无法知道地址背后是谁。
As an additional firewall, a new key pair should be used for each transaction to keep them from being linked to a common owner. Some linking is still unavoidable with multi-input transactions, which necessarily reveal that their inputs were owned by the same owner. The risk is that if the owner of a key is revealed, linking could reveal other transactions that belonged to the same owner.
作为额外的预防措施,每次交易都应该使用一个新的密钥对,以确保这些交易不被追溯到一个共同的所有者。但是由于并行输入(即很多笔交易同时转给一个地址)的存在,一定程度上的追溯还是不可避免的,因为这必然表明它们的输入由同一所有者拥有。此时的风险在于,如果某个人的某一个公钥被确认属于他,那么就可以追溯出此人的其它很多交易。
注解:
1 、总结:
这一章内容比较简单,主要解释了比特币是怎么保护使用者隐私的,关键就是匿名。使用者可以随机生成很多地址,利用这些地址来交易,只要你不实名承认这个地址是你的,就没法知道地址背后的真实身份。
但是在如今大数据 “ 发达 ” 并且干啥都要实名制的时代,“ 匿名 ” 又似乎是一个伪命题。理论上讲,交易所通过 KYC 认证依然可以追踪到你的每一笔交易。普通人对于匿名的需求并没有那么强,但是总会觉得能够实现匿名是一个更 “ 美好 ” 的世界。匿名的需求依然很大,比 bitcoin 匿名性更强的门罗币也是市值前十的主流币。
11. Calculations
We consider the scenario of an attacker trying to generate an alternate chain faster than the honest chain. Even if this is accomplished, it does not throw the system open to arbitrary changes, such as creating value out of thin air or taking money that never belonged to the attacker. Nodes are not going to accept an invalid transaction as payment, and honest nodes will never accept a block containing them. An attacker can only try to change one of his own transactions to take back money he recently spent.
11. 计算
我们设想一下这个场景:一个攻击者试图以比诚实(或可信)节点产生链条更快的速度来生成一个替代链条。即便他达到了这一目的,但是整个系统也并非就此完全对任意的变化开放( “ 完全对任意的变化开放 ” 可理解为 “ 完全被攻击者控制 ” ),比方说凭空创造价值,或者掠夺本不属于攻击者的货币。这是因为节点不会接受无效的交易信息作为付款信息,诚实(或可信)的节点也永远不会接受一个包含了无效交易信息的区块。一个攻击者能做的仅仅是篡改他自己的交易信息,来试图拿回他刚刚支付给别人的货币。
The race between the honest chain and an attacker chain can be characterized as a Binomial Random Walk. The success event is the honest chain being extended by one block, increasing its lead by +1, and the failure event is the attacker’s chain being extended by one block, reducing the gap by -1.
诚实链条和攻击者链条之间的竞赛,可以用二叉树随机漫步( Binomial Random Walk )来描述。成功事件定义为诚实链条被延长了一个区块,使其领先优势 + 1 ,而失败事件则是攻击者的链条被延长了一个区块,使得差距 – 1 。
The probability of an attacker catching up from a given deficit is analogous to a Gambler’s Ruin problem. Suppose a gambler with unlimited credit starts at a deficit and plays potentially an infinite number of trials to try to reach breakeven. We can calculate the probability he ever reaches breakeven, or that an attacker ever catches up with the honest chain, as follows [8]:
攻击者成功填补上某一既定差距的可能性,可以近似地看做赌徒破产问题( Gambler’s Ruin problem )。假定一个赌徒拥有可无限透支的信用,然后开始进行潜在次数为无穷的赌博,试图填补上自己的亏空。那么我们可以计算他填补上亏空的概率,也就是该攻击者赶上诚实链条(的概率),如下所示[8] :
p = probability an honest node finds the next block
q = probability the attacker finds the next block
= probability the attacker will ever catch up from z blocks behind
p = 诚实(或可信)节点找到(或生成)下一个区块的概率
q = 攻击者找到(或生成)下一个区块的概率
= 攻击者将从后面的第 z 个区块赶上的概率
注解:
1 、由上述等式可知:
- 如果 ,即诚实节点生成区块的概率小于或等于攻击者生成区块的概率,则攻击者赶上的概率是 100 % ;
- 如果 ,即诚实节点生成区块的概率大于攻击者生成区块的概率,则攻击者赶上的概率是 ,z 表示攻击者落后于诚实节点 z 个区块。
Given our assumption that , the probability drops exponentially as the number of blocks the attacker has to catch up with increases. With the odds against him, if he doesn’t make a lucky lunge forward early on, his chances become vanishingly small as he falls further behind.
我们假定 ,那么攻击成功的概率会随着区块数量的增加而呈现指数级下降。因为概率没有站在攻击者一方, 如果攻击者不能很幸运地迅速追赶上诚实(或可信)节点,那么攻击成功的概率将会越来越渺茫。
We now consider how long the recipient of a new transaction needs to wait before being sufficiently certain the sender can’t change the transaction. We assume the sender is an attacker who wants to make the recipient believe he paid him for a while, then switch it to pay back to himself after some time has passed. The receiver will be alerted when that happens, but the sender hopes it will be too late.
我们现在考虑一下收款人在收到转账后需要等待多长时间才能确认付款人已经无法篡改这笔交易(如果交易能够篡改,那么付款人将能够拿回已经支付的货币)。我们假设付款人是一个攻击者,他希望让收款人在一段时间内相信他已经付过款了,在过去一段时间后再将支付出去的款项重新拿回来。在这种情况发生的时候收款人能够收到警告,但是付款人希望收到警告时已经太迟了。
The receiver generates a new key pair and gives the public key to the sender shortly before signing. This prevents the sender from preparing a chain of blocks ahead of time by working on it continuously until he is lucky enough to get far enough ahead, then executing the transaction at that moment. Once the transaction is sent, the dishonest sender starts working in secret on a parallel chain containing an alternate version of his transaction.
收款人生成一对新的秘钥,然后在付款人签名前不久才把公钥发送给付款人。这将可以防止以下情况:付款人预先准备好一个区块链然后持续地对此区块进行运算,直到他的区块链幸运地超越了诚实链条,方才立即执行支付。只要交易一旦发出,不诚实的发送者(即攻击者)就开始秘密地准备一条包含了该交易替代版本的平行链条。
The recipient waits until the transaction has been added to a block and z blocks have been linked after it. He doesn’t know the exact amount of progress the attacker has made, but assuming the honest blocks took the average expected time per block, the attacker’s potential progress will be a Poisson distribution with expected value:
收款人将等到这笔交易出现在区块中,并且还有 z 个区块跟在它后面。此时,他仍然不能确切知道攻击者已经进展了多少个区块,但是假设诚实区块将耗费平均预期时间以产生一个区块(或理解为:但是假设诚实节点生成每个区块的时间是固定的话),那么攻击者的潜在进展就是一个泊松分布,该分布的期望值为:
To get the probability the attacker could still catch up now, we multiply the Poisson density for each amount of progress he could have made by the probability he could catch up from that point:
为了得出攻击者依然能够追赶上(诚实节点)的概率,我们将他可能取得的每一个进展的泊松密度乘以他从那一点追赶上的概率:
Rearranging to avoid summing the infinite tail of the distribution…
重新排列(或化为如下形式),以避免对分布的尾部进行无限求和 …
Converting to C code…
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
转换为 C 语言代码 …
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
Running some results, we can see the probability drop off exponentially with z.
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
经过计算,(可以看到攻击节点追上诚实节点的)概率 P 随着 z 值(落后的区块数量)的增加而呈指数级下降。
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
Solving for P less than 0.1%…
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
求解当 P 小于 0.1 %(时 z 的值)…
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
注解:
1 、如何通俗理解赌徒破产问题( Gambler’s Ruin problem )?
这一章主要是计算攻击者可以成功攻击的概率。由于计算过程比较复杂,我们可以简单地把这个攻击问题和 “ 赌徒破产 ” 问题进行类比。
假设两个赌徒 A 和 B ,分别有 M 和 N 个筹码,两个人掷骰子,123 则 A 赢,456 则 B 赢,赢的人可以得到对方 1 个筹码。一直进行下去,知道某一方输光为止。
这种情况下,A 和 B 赢得每一把赌博的概率是相等的(都是 50 % ),所以两人谁能笑到最后,就看谁手上的筹码更多。A 能赢的概率 = ,B 能赢的概率 = 。如果 M = N ,那么双方的获胜概率都是一样的(即 50 % )。理想情况下,双方的筹码相等,每一把获胜的概率相等,则双方最终获胜的概率也相等。
但现实情况通常是你的筹码不如赌场,每一把获胜的概率肯定没有 50 % ,在筹码和单次赌博的概率都处于劣势时,想从赌场手中赢钱无异于痴人说梦。而赌场所需要做的只是重复操作,一次次的赌,不需要做其他手脚,概率自然会将你的钱全部送到赌场的口袋里。因为赌场和概率站在一起,而赌徒站在了概率的对立面。
而攻击者就像是这样一个赌徒,诚实(或可信)节点们就像是赌场。攻击者的筹码不如诚实(或可信)节点(没有 51 % 以上的算力),攻击者每次攻击成功的概率没有 50 % ,所以想要攻击成功的概率极低。随着落后诚实(或可信)节点的区块数量越来越多,成功的概率也越来越小(呈现指数级下降)。
12. Conclusion
We have proposed a system for electronic transactions without relying on trust. We started with the usual framework of coins made from digital signatures, which provides strong control of ownership, but is incomplete without a way to prevent double-spending. To solve this, we proposed a peer-to-peer network using proof-of-work to record a public history of transactions that quickly becomes computationally impractical for an attacker to change if honest nodes control a majority of CPU power. The network is robust in its unstructured simplicity. Nodes work all at once with little coordination. They do not need to be identified, since messages are not routed to any particular place and only need to be delivered on a best effort basis. Nodes can leave and rejoin the network at will, accepting the proof-of-work chain as proof of what happened while they were gone. They vote with their CPU power, expressing their acceptance of valid blocks by working on extending them and rejecting invalid blocks by refusing to work on them. Any needed rules and incentives can be enforced with this consensus mechanism.
12. 结论
我们在此提出了一种不需要信用中介的电子支付系统。我们首先讨论了通常以数字签名为基础构建的电子货币架构,虽然这种架构为所有权提供了强有力的控制,但是不足以防止双重支付。为了解决这个问题,我们提出了一种采用工作量证明机制的点对点网络来记录公开的交易历史(或交易信息),如果诚实(或可信)节点能够控制绝大多数的 CPU 计算能力,那么攻击者通过计算来改变交易记录将变得不切实际。该网络的健壮之处在于它结构上的简洁性。节点之间的工作大部分是彼此独立的,只需要很少的协同。每个节点都不需要明确自己的身份,因为交易信息不会被路由到任何特定的地方,所以只需要尽其最大努力传播即可。节点可以随时离开和重新加入网络,并将(最长的)工作量证明链条作为在该节点离线期间发生的交易的证明。节点们用自己掌握的 CPU 资源来投票,通过在有效块上进行运算并延长它们来表示节点们接受这些有效块,通过拒绝对无效块进行处理来表示节点们拒绝这些无效块。任何必要的规则和激励措施都可以通过这种共识机制来执行。
注解:
1 、总结:
“ 结论 ” 这章的内容基本上是对前面所有章节的一个总结,看懂前面的内容,再看结论有一种 “ 他乡遇故知 ” 的感觉。前面每一章的标题就是白皮书的关键词,理解好这些关键词的意思,对于理解比特币和区块链就能有一个更深入的认识了。
比特币原版白皮书最后一章结束了,从最开始的摘要到最后的结论,每一次阅读都有不一样的感觉,就像碰到熟人一样,既有熟悉感,还有一点陌生感。文笔虽无文学之美,但是有逻辑和结构之美,读原文也比译文更能理解作者的意图。
中本聪是站在了巨人的肩膀上发明了比特币,将前人的密码学、经济学、数学等等知识融会贯通,发明了比特币。每当我们对区块链、比特币或者其他 XX 币、XX 链有所疑惑时,不妨追根溯源,再回过头来看看这份白皮书,相信一定会有所收获的。
2 、所以,你觉得比特币和区块链技术是泡沫吗?
正如本文开头的第一句话:“ 精英在做啤酒,平民在吹泡沫,骗子在割韭菜 ” 。
所以其他的产品是不是 “ 骗子 ” 不清楚,但是比特币和区块链技术不是泡沫。
References
[1] W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimal
trust requirements,” In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” In Journal of Cryptology, vol 3, no
2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping,”
In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, “Secure names for bit-strings,” In Proceedings of the 4th ACM Conference
on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, “Hashcash – a denial of service counter-measure,”
http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, “Protocols for public key cryptosystems,” In Proc. 1980 Symposium on Security and
Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, “An introduction to probability theory and its applications,” 1957.
引用
[1] W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998.(一种能够借助电子假名在群体内部相互支付并迫使个体遵守规则且不需要外界协助的电子现金机制)
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, “在最小化信任的基础上设计一种时间戳服务器” In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, “怎样为电子文件添加时间戳” In Journal of Cryptology, vol 3, no
2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, “提升电子时间戳的效率和可靠性”
In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, “比特字串的安全命名” In Proceedings of the 4th ACM Conference
on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, “哈希现金 — 拒绝服务式攻击的克制方法”
http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, “公钥密码系统的协议” In Proc. 1980 Symposium on Security and
Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, “概率学理论与应用导论” 1957.
英文原版的 PDF 下载请点击这里。
参考自:
- 原文:https://bitcoin.org/bitcoin.pdf
- 中文翻译参考自:https://www.8btc.com/wiki/bitcoin-a-peer-to-peer-electronic-cash-system/ ,有大量修改
- 中文翻译参考自:https://www.jianshu.com/p/9be5ac3725fc ,有大量修改

发表评论?