绪论：加法原理、乘法原理

分类计数原理：完成一件事，有 类办法，在第 1 类办法中有 种不同的方法，在第 2 类办法中有 种不同的方法 … 在第 类办法中有 种不同的方法，那么完成这件事共有 种不同的方法。

分步计数原理：完成一件事，需要分成 个步骤，做第 1 步有 种不同的方法，做第 2 步有 种不同的方法 … 做第 步有 种不同的方法，那么完成这件事共有 种不同的方法。

区别：分类计数原理是加法原理，不同的类加起来就是我要得到的总数；分步计数原理是乘法原理，是同一事件分成若干步骤，每个步骤的方法数相乘才是总数。

排列问题（需要排序）

排列数

从 个不同元素中取出 个元素的所有不同排列的个数，叫做从 个不同元素中取出 个元素的排列数，用符号 表示。

排列数公式

规定

排列数推导

把 个不同的元素任选 个排序，按计数原理分步进行：

取第一个：有 种取法；
取第二个：有 种取法；
取第三个：有 种取法；
……
取第 个：有 种取法；

根据分步乘法原理，得出上述公式。

排列数性质

可理解为：“ 某特定位置 ” 先安排，再安排其余位置。

可理解为：含特定元素的排列有 ，不含特定元素的排列有 ，具体解释如下所示：

以 为例， 表示在数列 “ 123 ” 中找到两个元素进行排序，共有下列 6 个排列：

12 13 21 23 31 32

假设不包含 3 这个特定元素，不含特定元素的排列有 ，那么就是指的 12 和 21 ，也就是相当于从数列 “ 12 ” 中取出 2 个元素进行排列；含特定元素的排列有 ，那么就是指的 13 、23 、31 和 32 ，也就是相当于从两个数列 “ 12 ” 和 “ 12 ” 中取出 1 个元素进行排列（把数列中的 “ 3 ” 全部挖掉）。

组合问题（不需要排序）

组合数

从 个不同元素中取出 个元素的所有不同组合的个数，叫做从 个不同元素中取出 个元素的组合数，用符号 表示。

组合数公式

组合数推导

利用排列和组合之间的关系以及排列的公式来推导证明。

将部分排列问题 分解为两个步骤：

第一步，就是从 个球中抽 个出来，先不排序，此即组合数问题 ：

第二步，则是把这 个被抽出来的球进行排序，即全排列 。

根据乘法原理， ，那么：

组合数性质

 可以理解为：将原本的每个组合都反转，把原来没选的选上，原来选了的去掉，这样就变成从 个元素中取出 个元素，显然方案数是相等的。

递推公式 可理解为：含特定元素的组合有 ，不含特定元素的组合有 ，具体解释如下所示：

以 为例， 表示在数列 “ 12345 ” 中找到两个元素的组合，共有下列 10 个组合：

12 13 14 15 23 24 25 34 35 45

假设不包含 1 这个特定元素，不含特定元素的组合有 ，那么就是指的 23 、24 、25 、34 、35 和 45 ，也就是相当于从数列 “ 2345 ” 中取出 2 个元素进行组合；含特定元素的组合有 ，那么就是指的 12 、13 、14 和 15 ，也就是相当于从数列 “ 2345 ” 中取出 1 个元素进行组合（把数列中的 “ 1 ” 全部挖掉）。

组合数求和公式

我们感性认知一下，上面这个式子的左边表示什么呢？

把从 个球中抽出 0 个球的组合数（值为 1 ）、抽出 1 个球的组合数、抽出 2 个球的组合数 … 抽出 个球的组合数相加。

换句话说，就是从 个球中随便抽出一些不定个数的球，问一共有多少种组合。

对于第 1 个球，可以选，也可以不选，有 2 种情况；
对于第 2 个球，可以选，也可以不选，有 2 种情况；
对于任意一个球，可以选，也可以不选，有 2 种情况。

根据乘法原理，一共 种组合。

组合数求和公式推导

想要严谨的证明？可用数学归纳法：

1 、当 时， 成立。

2 、假设 时等式成立，即

当 时，

等式也成立。

3 、由 1 和 2 得，等式对 都成立。

也可偷懒地用二项式定理证明（其实二项式定理也是用数学归纳法证明的）：

令 ，就得到了：

杨辉三角

这个神奇的图形和组合数、二项式定理密切相关。

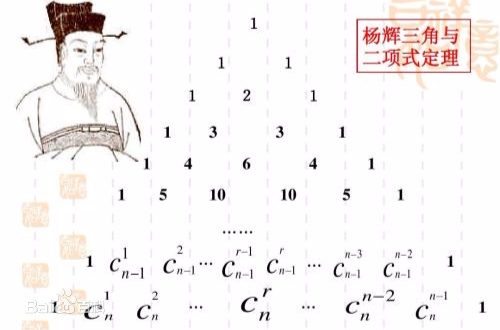
杨辉三角可以帮助你更好地理解和记忆组合数的性质：

1. 第 行的第 个数可表示为 ，即为从 个不同元素中取 个元素的组合数；
2. 第 行的数字有 项；
3. 每行数字左右对称（第 行的第 个数和第 个数相等，），由 1 开始逐渐变大；
4. 每个数等于它上方两数之和（第 行的第 个数等于第 行的第 个数和第 个数之和，即 ）；
5. 的展开式中的各项系数依次对应杨辉三角的第 行中的每一项（二项式定理）。

 

转自：

• https://www.cnblogs.com/1024th/p/10623541.html