更多有关于 “ 量子通信 ” 的文章，请点击这里。

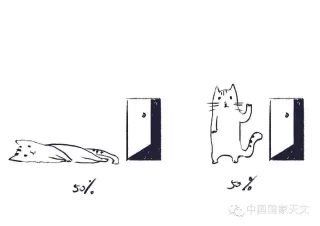
导读：在 |0> 和 |1> 的基组中测量 |+> = ( |0> + |1> ) / √2 ，如果你把这个实验重复很多次，那么可以预测你有接近一半的次数得到 |0> ，接近一半的次数得到 |1> 。但对于单独的一次实验，你没办法做出任何预测。同样的原因可以导致不同的结果！这种内在的随机性是量子力学的本质特征。

上一篇文章《你完全可以理解量子信息（之一）》

六 、第二大奥义：测量

在经典力学中，测量固然是一种重要的操作，但我们不会认为测量过程跟其他过程服从不同的物理规律。无论你看或不看某个物体，你都相信它具有某些确定的性质，如位置、速度，而且你看了以后这些性质不会变化。总之，你可以随便看。

可是在量子力学中，测量跟其他过程有本质的区别，描述测量要用与众不同的物理规律！你不能随便看了，你看或不看某个体系，会造成很大的区别。

量子力学中的测量，特殊在哪里呢？

首先，在量子力学中，每一次测量都必须对应某个基组。两次测量可以用不同的基组，比如你可以这次用 |0> 和 |1> ，下次用 |+> 和 |-> ，这是允许的，但每次你都必须确定当前用的是哪个基组。

确定了基组，然后呢？这时有两种情况，取决于待测量的态是不是基组中的一个态。如果是，那么测量后这个态不变。比如说在 |0> 和 |1> 的基组中测量 |0> ，必然得到 |0> 。

然而，如果待测量的态不是基组中的一个态，比如说在 |0> 和 |1> 的基组中测量 a|0> + b|1> ，其中 a 和 b 都不等于 0 ，也就是说这个态既不是 |0> 也不是 |1> ，会怎么样？

答案是：这个态会发生突变！也常有人把这个突变称为 “ 塌缩 ” 、“ 坍缩 ” 或类似的词。这个突变是瞬间发生的，是一个真正意义上的突然变化。

变成什么？变成基组中的一个态，即 |0> 或 |1> 中的某一个。更具体地说，以 |a|² 的概率变成 |0> ，以 |b|² 的概率变成 |1> 。请注意，我们无法预测特定的某次测量变成 |0> 还是 |1> ，能预测的只是概率。由于只可能有这两种结果，所以这两个概率相加等于 1 ，这就是 |a|² + |b|² = 1 的原因。

上一节中说，一个电子可以 “ 同时位于两个地方 ” 。实际的意思就是，一个电子可以处于两个位置的叠加态，测量它的位置时，会以一定的概率发现它位于这里，以一定的概率发现它位于那里。

测量导致状态突变之后，再在同样的基组下测量，就回到了第一种情况（待测的态是基组中的一个态），所以就不会变了。也就是说，如果你第一次测得的是 |0> ，那么以后你再在 |0> 和 |1> 的基组中测量多少次，都仍然是 |0> ；如果你第一次测得的是 |1> ，那么以后你再在 |0> 和 |1> 的基组中测量多少次，都仍然是 |1> 。

我们可以把测量理解为强迫叠加态 “ 削足适履 ” ：给你一组状态，跟你都不一样，而你必须在其中选择一个，就只好随机挑了。

八仙中铁拐李的故事，用在这里意外的合拍。铁拐李原本是一位翩翩公子，F4 级别的帅哥。由于修仙有成，应邀去参加太上老君的 “ 学术活动 ” 。临走时，他告诉学生自己要元神出窍七天，要学生照看好自己的身体。参加完学术活动回来，却发现学生已经把自己的身体火化了。（难道是因为考试没给他过？）这时鸡马上就要叫，如果他找不到可附体的对象就要魂飞魄散。这时他发现周围有几个可附的尸体，他只得在其中随便选择一个！（原来的故事是只有一个尸体，但一个基组至少要有两个态可供选择。）不料是个拐子，于是帅哥李就变成了铁拐李。结论是：学术活动害死人 ……（大误）

猪八戒：喂喂喂，你的运气已经不错啦，不要不知足！早跟你说了，投胎是个技术活儿！其实跟投胎相比，撞天婚是我更喜欢的 “ 测量 ” ，只可惜真真、爱爱、怜怜是个假的 “ 基组 ” ……

测量中的突变，意味着我们对因果律的理解需要改变。举个例子，在 |0> 和 |1> 的基组中测量 |+> = ( |0> + |1> ) / √2 ，会以一半的概率得到 |0> ，一半的概率得到 |1> 。概率的意思是，如果你制备很多个处于 |+> 的体系，把这个实验重复很多次，那么可以预测你有接近一半的次数得到 |0> ，接近一半的次数得到 |1> 。但对于单独的一次实验，你没办法做出任何预测。是的，同样的原因可以导致不同的结果！

这种内在的随机性是量子力学的一种本质特征。在经典力学中，一切演化都是决定性的，同样的原因必然导致相同的结果，量子力学却不是这样。

有人在这里可能要问：经典力学中也有随机性，掷硬币不就是一半概率朝上，一半概率朝下吗？回答是：同样叫做概率，背后的原因不一样，可改进的余地也不一样。

掷硬币的结果难以预测，是因为相关的外界因素太多：硬币出手时的方位、速度、空中的气流状况等等。也就是说，经典力学中的概率反映的是信息的缺乏。你可以通过减少这些因素的干扰来增强预测能力，例如在真空中掷、消灭气流、用机器掷、固定方向和力度。最终，你可以确定地掷出某一面，或者至少使掷出某一面的机会显著超过另一面。（赌神是怎样炼成的！）

但在量子力学中，测量结果的概率是由体系本身的状态决定的，不是由于外界的干扰，不是由于缺少任何信息，因此完全无法 “ 改进 ” 。给你一个处于 |+> 的粒子，问你有什么办法保证这次在 |0> 和 |1> 的基组中测量它时得到 |0> ，回答只能是：没有任何办法。（卡门：爱情是一只不羁的鸟儿，任谁都无法驯服 …… ）所以再次强调，这种随机性是内在的，是量子力学的一种本质特征！

导读：没有人知道量子纠缠的机制？这是个常见的误解。其实量子纠缠是一个被理论预言然后确实观察到了的现象，而不是意外的实验发现，所以，科学家怎么可能不知道它的机制呢？量子纠缠的机制就是：叠加原理，测量时的突变，以及直积态和纠缠态的区别。

七 、第三大奥义：纠缠

前面说的都只是一个量子比特的体系，已经有这么多不可思议之处。多个量子比特的体系，可想而知会更加奇怪。这就引出了 “ 量子纠缠 ” 现象 —— 你听说过这个词，对不对？

量子纠缠在许多文章中被传得神乎其神，几乎成了心灵感应、神秘主义的代名词。但其实量子纠缠是一个有明确定义的概念，是一种被量子力学预言必然出现也早就观测到了的现象。它的物理原理很清楚，绝大部分神秘感都是被故弄玄虚的媒体强加上去的。看了下面的解释，你就明白它实际上是什么了。

我们先来看一个数学问题。拿出一个二元函数 F ( x , y ) ，你来试着把它写成一个关于 x 的函数 f ( x ) 与一个关于 y 的函数 g ( y ) 的乘积，也就是说，寻找 f ( x ) 和 g ( y ) ，使得 F ( x , y ) = f ( x ) g ( y ) 。如果可以，我们就说 F ( x , y ) 是可以 “ 分离变量 ” 的。如果不行，我们就说它不能分离变量。同样的定义可以推广到二元以上的函数，例如 F ( x , y , z ) 是否可以写成 f ( x ) g ( y ) u ( z ) ，就是这个三元函数能不能分离变量。

显然，有些二元函数是可以分离变量的。例如 F ( x , y ) = xy ，你取 f ( x ) = x 和 g ( y ) = y 就可以了。（这是道送分题！）又如 F ( x , y ) = xy + x + y + 1 ，仔细看看你就会发现它等于 ( x + 1 ) ( y + 1 ) ，所以取 f ( x ) = x + 1 和 g ( y ) = y + 1 即可。

然而，如果 F ( x , y ) = xy + 1 呢？这时你就会发现，无论如何也不能把它表示成 f ( x ) g ( y ) 。

对此可以用反证法证明如下：假设 F ( x , y ) = f ( x ) g ( y ) ，那么对 y 取两个值 y₁ 和 y₂ 时，F ( x , y₁ ) = f ( x ) g ( y₁ ) ，F ( x , y₂ ) = f ( x ) g ( y₂ ) 。这两个式子相除，就会把 f ( x ) 消掉，得到 F ( x , y₁ ) / F ( x , y₂ ) = g ( y₁ ) / g ( y₂ ) 。等式的右边 g ( y₁ ) / g ( y₂ ) 是一个与 x 无关的数，因此等式的左边 F ( x , y₁ ) / F ( x , y₂ ) 也必须是个与 x 无关的数。可是对于 F ( x , y ) = xy + 1 ，设 y₁ = 0 ，得到 F ( x , y₁ ) = 1 ，设 y₂ = 1 ，得到 F ( x , y₂ ) = x + 1 。两者相除得到 F ( x , y₁ ) / F ( x , y₂ ) = 1 / ( x + 1 ) ，跟 x 有关。因此初始的假设不对，F ( x , y ) = xy + 1 不能分离变量。

有了以上的数学准备，我们就可以解释量子纠缠是什么了。

在量子力学中，体系的状态（没错，就是前面说的态矢量）可以用一个函数来表示，称为 “ 态函数 ”（是的，你既可以把它理解为一个函数，也可以把它理解为一个矢量，两者不矛盾，怎么方便怎么来）。单粒子体系的态函数是一元函数，多粒子体系的态函数是多元函数。如果这个多元函数可以分离变量，也就是可以写成多个一元函数直接的乘积，我们就把它称为 “ 直积态 ” 。如果它不能分离变量，我们就把它称为 “ 纠缠态 ” 。

直积态和纠缠态的区分为什么重要？我们举些例子来说明。

在量子力学中，我们常常用类似 |00> 的狄拉克符号来表示两粒子体系的状态，其中第一个符号表示粒子 1 所处的状态，第二个符号表示粒子 2 所处的状态，|00> 就表示两个粒子都处于自己的 |0> 态。同理，|01> 表示粒子 1 处于自己的 |0> 态、粒子 2 处于自己的 |1> 态，|11> 表示两个粒子都处于自己的 |1> 态，如此等等。

这些状态都是直积态，体系整体的二元态函数就是两个粒子各自的一元态函数的乘积。对于直积态，你在测量粒子 1 的时候，不会影响粒子 2 的状态，所以你可以说 “ 粒子 1 处于某某状态，粒子 2 处于某某状态 ” 。这就是分离变量的结果。

下面我们来考虑这样一个状态：|β00> = ( |00> + |11> ) / √2 ，它是 |00> 和 |11> 的一个叠加态（是的，叠加原理对多粒子体系也成立）。这个态是不是直积态呢？也就是说，( |00> + |11> ) / √2 能不能写成 ( a|0> + b|1> ) ( c|0> + d|1> )（前一个括号中是粒子 1 的状态，后一个括号中是粒子 2 的状态）？

你立刻就会发现，不能。假如可以的话，因为这个状态中不包含 |01> ，所以 ad = 0 ，于是 a 和 d 中至少有一个等于 0 。但是如果 a = 0 ，|00> 就不会出现；而如果 d = 0 ，|11> 又不会出现。无论如何都自相矛盾，所以假设错误，|β00> 不是直积态，而是纠缠态，不能分离变量。这就意味着，不能用 “ 粒子 1 处于某某状态，粒子 2 处于某某状态 ” 这样的语言来描述 |β00> ，你只能说这个体系整体处于 |β00> 状态。

真正惊人的事情，发生在对 |β00> 做测量的时候。你对它测量粒子 1 的状态，会以一半的概率使整个体系变成 |00> ，此时两个粒子都处于自己的 |0> ；以一半的概率使整个体系变成 |11> ，此时两个粒子都处于自己的 |1> 。你无法预测单次测量的结果，但你可以确定，粒子 1 变成什么，粒子 2 也就同时变成了什么。两者总是同步变化的。好比成龙的电影《双龙会》中有心灵感应的双胞胎，一个做了某个动作，另一个无论相距多远都会做同样的动作。

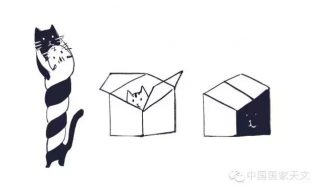
在许多科普文章中，也经常用另一个态 ( |01> + |10> ) / √2 作例子，我们可以把它记为 |β01> 。这个态的特点是，你对它测量粒子 1 的状态，会以一半的概率发现粒子 1 处于 |0> ，粒子 2 处于 |1> ，另一半概率发现粒子 1 处于 |1> ，粒子 2 处于 |0> 。你无法预测单次测量的结果，但你可以确定，粒子 1 变成什么，粒子 2 就同时变成了相反的状态。下面的漫画表现的就是这个态。

有趣的是，纠缠这个重要的量子力学现象，是由几位反对量子力学的科学家提出的，而且其中的 “ 带头大哥 ” 就是爱因斯坦！

如前所述，爱因斯坦是量子力学早期的奠基人之一。实际上，他得诺贝尔奖不是因为提出相对论，而是因为提出光量子（即光子）理论（这是诺贝尔奖委员会做过的最搞笑的事情之一）。但随着量子力学的发展，爱因斯坦对量子力学的许多特性产生了深深的怀疑。

他认为每个粒子在测量之前都应该处于某个确定的状态，而不是等到测量之后，否则就不能叫做 “ 物理实在 ” 。爱因斯坦的一个经典问题是：“ 你是否相信，月亮只有在我们看它的时候才存在？”

1935 年，爱因斯坦（ Albert Einstein ）、波多尔斯基（ Boris Podolsky ）和罗森（ Nathan Rosen ）提出了一个思想实验，后人用他们姓的首字母把他们三人合称为 EPR 。先让两个粒子处于 |β00> 态，这样一对粒子称为 “ EPR 对 ” 。把这两个粒子在空间上分开很远，可以任意的远。然后测量粒子 1 。如果你测得粒子 1 在 |0> ，那么你立刻就知道了粒子 2 现在也在 |0> 。

EPR 问：既然两个粒子已经离得非常远了，粒子 2 是怎么知道粒子 1 发生了变化，然后发生相应的变化的？EPR 认为两个粒子之间出现了 “ 鬼魅般的超距作用 ” ，信息传递的速度超过光速，违反了狭义相对论。所以，量子力学肯定有毛病。

这是个深邃的问题，量子力学的另一位奠基人玻尔为此跟爱因斯坦进行过激烈的辩论。玻尔的回答是：处于纠缠态的两个粒子是一个整体，绝不能把它们看作彼此独立无关的，无论它们相距有多远。当你对粒子 1 进行测量的时候，两者是同时发生变化的，并不是粒子 1 变了之后传一个信息给粒子 2 ，粒子 2 再变化。所以这里没有发生信息的传递，并不违反相对论。

仔细想一想，你就会明白 EPR 实验没有传输信息。如果 A 希望把一比特的信息 “ 0 ” 或 “ 1 ” 传给远处的 B ，那么双方需要事先约定好如何表示这个信息，比如说 A 想传 “ 0 ” 时就让 B 测得粒子 2 处于 |0> ，A 想传 “ 1 ” 时就让 B 测得粒子 2 处于 |1> 。假如 A 能控制测量的结果，比如说这次 A 一定会让粒子 1 处于 |0> ，那么 A 同时就让粒子 2 处于了 |0> ，A 确实就给 B 传了一个 “ 0 ” 。

但是，量子力学的精髓恰恰在于测量的结果是随机的，你不能控制，所以 EPR 实验不能这么用。A 测量粒子 1 得到的是一个随机数，B 测量粒子 2 得到的也是一个随机数，只不过这两个随机数必然相等而已。你想传一个比特，可是 EPR 对完全不听你指挥，所以你传不了任何信息。既然没传输信息，当然就不违反狭义相对论了。

在爱因斯坦和玻尔的时代，人们只能对 EPR 问题进行哲学辩论（这是好听的说法，说得通俗一点就是 “ 打口水仗 ”），无法通过实验做出判断。1964 年，贝尔（ John S. Bell ）指出，可以设计一种现实可行的实验，把双方的矛盾明确表现出来。对两粒子体系测量某些物理量之间的关联程度，如果按照 EPR 的观点，这些物理量在测量之前就有确定的值，那么这个关联必然小于等于 2 ；而按照量子力学，这个关联等于 2√2 ，大于 2 。这个 “ 关联小于等于 2 ” 的不等式叫做贝尔不等式，而量子力学不满足贝尔不等式。

从 1980 年代开始，阿斯佩克特（ Alain Aspect ）等一系列的研究组在越来越高的精度下做了实验，结果都是在很高的置信度下违反贝尔不等式，量子力学赢了。EPR 的思想实验最初是用来批驳量子力学的，结果却证实了量子力学的正确！

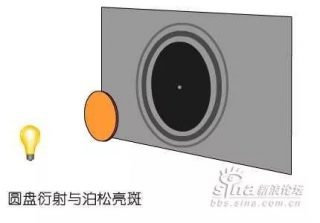
类似的故事在科学史上也常有。十九世纪的时候，泊松（ Simeon-Denis Poisson ）主张光是粒子，菲涅耳（ Augustin-JeanFresnel ）主张光是波动，两个阵营打得不可开交。1818 年，菲涅耳计算了圆孔、圆板等形状的障碍物产生的衍射花纹。泊松指出，按照菲涅耳的理论，在不透明圆板的正后方中央会出现一个亮点。从常识来看，不应该是暗的吗？于是泊松宣称波动说推出了荒谬的结果，已经被驳倒了。

但是菲涅耳和阿拉果（ Dominique F. J. Arago ）立即做实验，结果显示那里真的有一个亮斑（学过光学的同学能够理解，这是因为所有到达那里的衍射光都经过同样的路程，发生同相的叠加，互相加强）。于是波动说大获全胜，粒子说被打入冷宫（1905 年被爱因斯坦复活了，这就是他得诺贝尔奖的原因）。后人很有幽默意味地把这个亮点称为泊松亮斑。这正应了尼采的话：“杀不死我的，使我更强大！”

EPR 现象既然是一个真实的效应，而不是爱因斯坦等人以为的悖论，人们就想到利用它。现在，EPR 对是量子信息中一个非常有力的工具。对此我们只能说，伟人连错误都是很有启发性的！就像《大话西游》中的名言：跑都跑得那么帅~

现在科学家们认为，纠缠是一种新的基本资源，其重要性可以和能量、信息、熵或任何其他基本的资源相比。不过目前还没有描述纠缠现象的完整的理论，人们对这种资源的理解还远不够深入。有人把纠缠比喻为 “ 青铜时代的铁 ” ，它可能会在下一个历史时代大放异彩。

对量子纠缠的种种误解，经常出现在各种半吊子 “ 科普 ” 文章或者装神弄鬼的文章中。这里来稍稍解释一下。

最经常见到的误解是：量子纠缠是个非常神奇的现象，没有人知道它的机制是什么。

实际情况是：量子纠缠的机制就是上面说的这些，叠加原理，测量时的突变，直积态和纠缠态的区别。其实量子纠缠是一个被理论预言然后确实观察到了的现象，而不是意外的实验发现，所以，科学家怎么可能不知道它的机制呢？

如果你觉得这些不像个 “ 机制 ” ，那么请你想想，2 + 3 = 5 的机制又是什么？我们只能说，2 + 3 = 5 是自然数理论的必然推论，自然数理论就是它的机制。量子纠缠现象就是量子力学原理的必然推论，你不可能把量子力学之外的东西搞成它的机制。

经常有人脑洞大开地提议，量子纠缠的机制是，两个相距遥远的粒子在高维空间里连在一起，或者说它们的 “ 内部距离 ” 为零，我们平时看到的三维空间是高维空间的投影。这种说法看起来很机智，实际上没有什么用处。因为它完全是为了解释量子纠缠这一个现象而提出来的，而且只是定性解释，不能给出任何定量预测，也不能用到任何别的现象上。这只是一种语言游戏而已。

就像有的原始人看到飞机飞行觉得很神奇，造个理论说有一只大鸟的魂灵在这铁鸟里面托着它飞，在其他原始人看来好像很有道理，在内行看来却是多此一举。真要想理解飞机的原理，你就必须学空气动力学。同样，真要想理解量子纠缠的原理，你就必须学量子力学，舍此别无他途。

还有一种常见的误解，是以为任何两个粒子都会横跨整个宇宙同步变化。实际情况是，只有处于纠缠态的两个粒子才会这样。这是一个需要条件的现象，不是无条件的，而且在实验上精确制备这种条件还很不容易。

量子纠缠是一种多粒子体系的现象，而粒子越多，操纵起来当然就越困难。所以你会不时地看到这样的新闻：中国科学技术大学潘建伟团队实现了 x 个光子的纠缠态，刷新了以前同一研究组创造的 y 个光子纠缠的世界纪录。最新的 x = 10 ，y = 8 ，这是 2016 年 12 月的消息。多次打破世界纪录的撑杆跳高名将布勃卡和牙买加飞人博尔特，就是这个 feel！

最大而无当的误解，是以为量子纠缠证明了某种神秘主义的哲学或宗教，大发一通包罗万象、鬼话连篇的议论。实际情况是，量子纠缠是个原理很清楚的物理现象。你要拿它来讨论哲学或宗教，至少也该先搞清楚它是什么！

（坐等原博继续更新）

 

转自：

• http://blog.sciencenet.cn/blog-3277323-1101621.html
• http://blog.sciencenet.cn/blog-3277323-1116500.html